Необходимые и достаточные условия устойчивости линейных стационарных систем

Пусть известна математическая модель системы, описывающая свободное движение системы в виде однородного дифференциального уравнения:

(1)

или разностного уравнения

(1΄)

и пусть x — это отклонение интересующей нас переменной от её значения в равновесном режиме. Тогда система будет устойчива, если выполняется условие 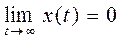(2)

или (2΄)

При каких условиях выполняется равенство (2)?

Уравнениям (1) и (1΄) соответствуют характеристические уравнения:

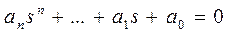… (3)

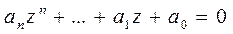… (3΄)

Если корни s_i уравнения (3) различны, то решение уравнения (1) может быть записано следующим образом .

В общем случае корни являются комплексными s_i=α_i+jβ_i.

1) Если α_k>0 A→∞ система не устойчива.

2) Если α_k<0 A→0 система устойчива.

3) Если α_k=0 A=c_k=const система нейтрально устойчива.

Следовательно, для устойчивости линейной непрерывной стационарной системы необходимо и достаточно, чтобы все корни характеристического уравнения имели отрицательные вещественные части, то есть располагались в левой полуплоскости плоскости S.

Можно показать, что для устойчивости дискретной линейной стационарной системы необходимо и достаточно, чтобы все корни характеристического уравнения (3΄) z_i были: |z_i|<1 … (!!)