Преобразование Лапласа непрерывных функций

Рассмотрим f₁(t)=f(t)e^-^ct, c=const такая, что:

(4)

При этом для существования этого интеграла от функции f(t) пришлось потребовать выполнения условия f(t)=0 t<0.

c>c₀ (c₀ — абсцисса абсолютной сходимости).

Для [1(t)] с₀=0

Для e^-α^tс₀=α

Для e^α^tс₀=-α

Для sinαt с₀=0

Тогда получим 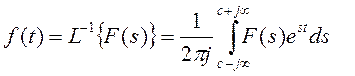(5)

Это интеграл Лапласа или формула обращения в преобразовании Лапласа.

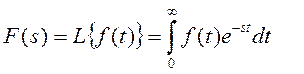(6)

f(t) F(s)

Дата добавления: 2015-01-02; просмотров: 654;