Частные производные высших порядков

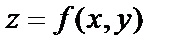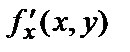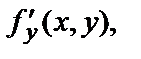Если функция определена в некоторой области D, то её частные производные и в свою очередь, будут функциями двух переменных 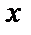и определёнными в той же области D или её части. Будем называть их частными производными первого порядка.

Частные производные 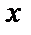по и по от функци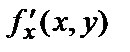й и 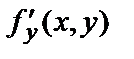в точке 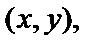если они существуют, называются частными производными второго порядка от функции 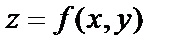в этой точке и обозначаются следующим образом:

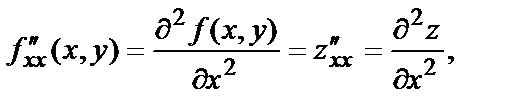
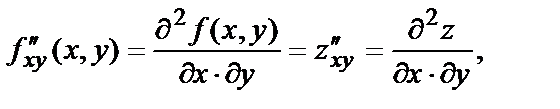
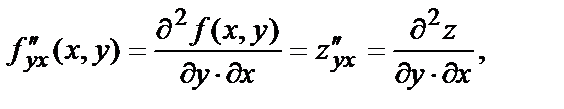
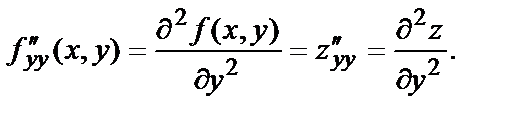
По определению

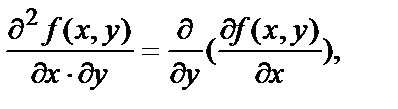т.е. производная, взятая по переменной y от производной функции 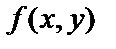по переменной х.

Частные произведения второго порядка зависят от координат точки, в которой они вычисляются, т.е., в свою очередь, являются функциями двух переменных. Так, например, для функции 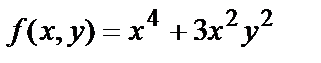в любой точке 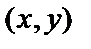плоскости имеем:

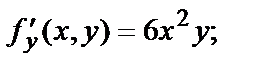
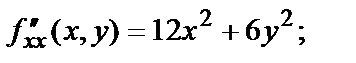
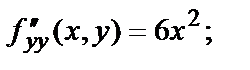
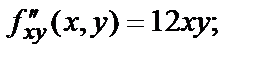
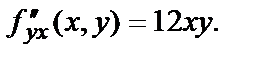
В заданных точках значения частных производных второго порядка:

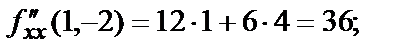
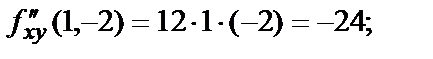
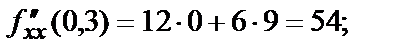
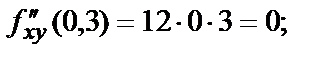
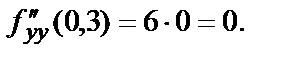
Частные производные третьего, четвёртого и пр. порядков вводятся аналогично. Так 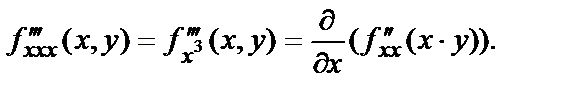На примерах вы видели, что 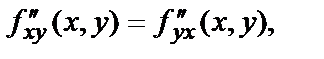т.е. смешанные частные производные функции, отличающиеся лишь последовательностью произведённых дифференцирований, совпадают друг с другом. Это справедливо, конечно, не для всех абсолютно функций. Если смешанные частные производные не являются непрерывными, то они существенно зависят от порядка дифференцирования. В нашей практике функции таковы, что смешанные частные производные не зависят от порядка дифференцирования, т.е., например,

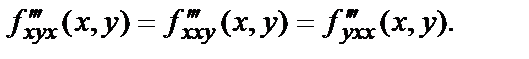
Для функции большего числа переменных понятие частных производных высших порядков аналогично.

Например, если 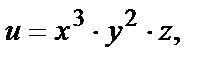то в любой точке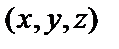

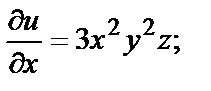
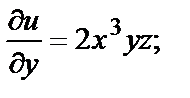
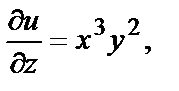
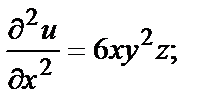
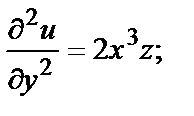
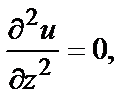
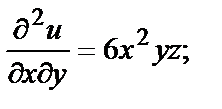
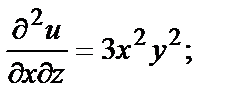
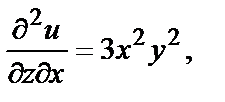
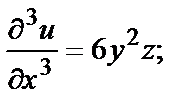
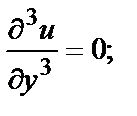
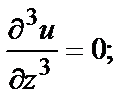
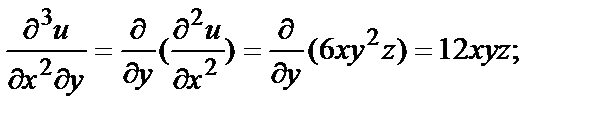
и т.д.

Пример № 1. Доказать, что функция 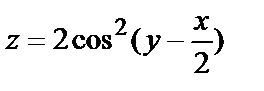удовлетворяет уравнению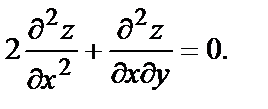

Найдём указанные производные, для чего начнём с частной производной по х:

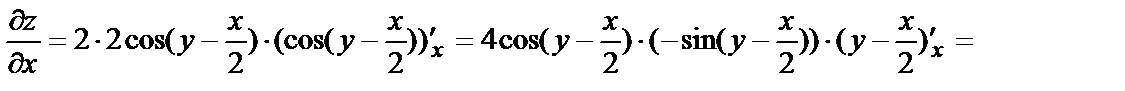
(Здесь использовали: ).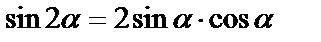

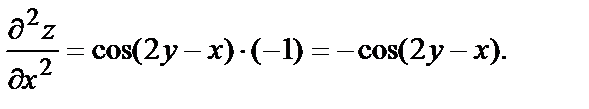
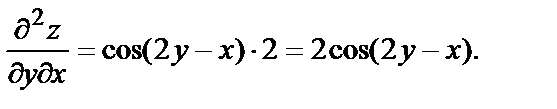
Подставим в уравнение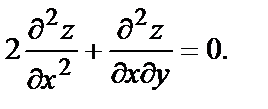

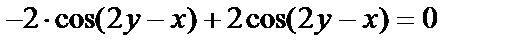- верно.