ТЕМА 7. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Настоящие учебно-методические материалы (тема 7) предназначены в помощь студентам для самостоятельного изучения дифференциального исчисления функции нескольких переменных и приложений.
Во многом дифференциальное исчисление функции нескольких переменных аналогично соответствующим разделам для функции одной переменной (тема 3). Разумеется, есть и отличительные особенности, которые при внимательном изучении легко обнаруживаются.
Изучение теории экстремумов необходимо для решения многих экономических задач, особенно в планировании производства: это экстремальные задачи на отыскание наиболее выгодного варианта, задачи нахождения наибольшего или наименьшего значения функции, зависящей от большого числа переменных.
В теме 7 дано изложение теории дифференциального исчисления функции двух переменных, снабжённое большим числом подробно разобранных примеров. Рассмотрены задачи геометрических и физических приложений.
Поскольку решение задач дифференциального исчисления функции двух переменных основывается на знании практически всего рассмотренного математического курса, предлагается заключительное экзаменационное задание.
Функции нескольких переменных. Основные понятия
До сих пор мы занимались изучением функции одной переменной, т.е. изучением величины, значения которой зависят от значений одной независимой переменной.
На практике приходится иметь дело с величинами, численные значения которых зависят от значений нескольких изменяющихся независимо друг от друга физических и геометрических величин. Изучение таких величин приводит к понятию функции нескольких переменных. Приведём несколько примеров.
Площадь S прямоугольника зависит от значений его длины x и ширины y и выражается формулой 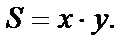 Каждой паре значений x и y соответствует определённое значение площади S; S – есть функция двух переменных x и y.
Каждой паре значений x и y соответствует определённое значение площади S; S – есть функция двух переменных x и y.
Объём V конуса есть функция его высоты h и радиуса r и выражается формулой 
Объём V прямоугольного параллелепипеда с рёбрами, длины которых равны x, y, z, выражается формулой  Здесь V – функция трёх переменных x, y, z.
Здесь V – функция трёх переменных x, y, z.
Начнём с простейшего случая, когда дана функция двух независимых переменных. Почти все понятия, касающиеся функции двух переменных, являются обобщениями соответствующих понятий для функции одного переменного.
Определение. Переменная z называется функцией двух переменных x и y, если каждой паре (x,y) из некоторого множества по определённому закону поставлено в соответствие значение переменной z.
При этом переменные x и y называются независимыми переменными или аргументами, а переменная z – зависимой переменной или функцией.
Записывают: 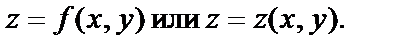
Определение. Множество пар чисел (х,у), для которых определена функция z, называется областью определения этой функции.
Так как каждой паре (х,у) из области определения функции z на плоскости соответствует точка М(х,у), то функцию 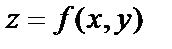 можно рассматривать как функцию переменной точки М(х,у) и обозначать
можно рассматривать как функцию переменной точки М(х,у) и обозначать  Область определения функции двух переменных геометрически представляет собой множество точек плоскости. И сама функция двух переменных допускает геометрическую интерпретацию.
Область определения функции двух переменных геометрически представляет собой множество точек плоскости. И сама функция двух переменных допускает геометрическую интерпретацию.
Пусть функции 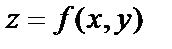 определена в некоторой плоской области D. Рассмотрим тройку чисел x, y, z, где
определена в некоторой плоской области D. Рассмотрим тройку чисел x, y, z, где 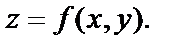 Этой тройке в пространстве соответствует единственная точка Р(х,у,z) с координатами x, y, z.
Этой тройке в пространстве соответствует единственная точка Р(х,у,z) с координатами x, y, z.
Множество всех таких точек Р(х,у,z) пространства называется графиком функции 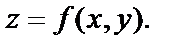 Чаще всего этот график представляет собой поверхность, а равенство
Чаще всего этот график представляет собой поверхность, а равенство 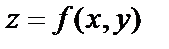 называют уравнением этой поверхности. Уравнению поверхности удовлетворяют координаты точек данной поверхности и не удовлетворяют координаты других точек пространства.
называют уравнением этой поверхности. Уравнению поверхности удовлетворяют координаты точек данной поверхности и не удовлетворяют координаты других точек пространства.
Простейшую поверхность – плоскость, которая задаётся уравнением  можно рассматривать как график функции
можно рассматривать как график функции  (для этого надо разрешить уравнение
(для этого надо разрешить уравнение 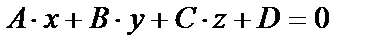 относительно z). Область определения функции
относительно z). Область определения функции  при любых числах n, m, p является множеством всех точек М(х,у) координатной плоскости, т.е. -¥<x<+¥, -¥<у<+¥.
при любых числах n, m, p является множеством всех точек М(х,у) координатной плоскости, т.е. -¥<x<+¥, -¥<у<+¥.
Рассмотрим несколько примеров
№ 1.  Эта функция определена при любых x и любых у, т.е. область её определения -¥<x<+¥, -¥<у<+¥.
Эта функция определена при любых x и любых у, т.е. область её определения -¥<x<+¥, -¥<у<+¥.
№ 2.  Эта функция определена лишь для неотрицательных значений подкоренного выражения, т.е. когда
Эта функция определена лишь для неотрицательных значений подкоренного выражения, т.е. когда 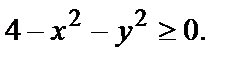 Отсюда найдём область определения:
Отсюда найдём область определения: 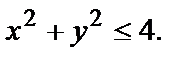 Последнее выполняется для всех точек, лежащих на окружности
Последнее выполняется для всех точек, лежащих на окружности 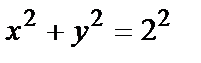 и внутри неё. Центр окружности т. О(0,0), радиус окружности r=2. (рис. 1).
и внутри неё. Центр окружности т. О(0,0), радиус окружности r=2. (рис. 1).
№ 3. 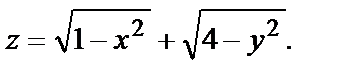 Область определения этой функции найдём из условия одновременного выполнения двух неравенств
Область определения этой функции найдём из условия одновременного выполнения двух неравенств 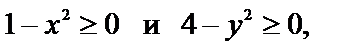 т.е. из системы
т.е. из системы
 или
или 
Получаем множество точек прямоугольника со сторонами
х=1; х= –1; у=2; у= –2 (рис. 2).
№ 4.  Область определения этой функции найдём из неравенства
Область определения этой функции найдём из неравенства  или
или  Это точки плоскости, лежащие вне окружности с центром в точке О(0,0) и радиусом r=1 (рис. 3).
Это точки плоскости, лежащие вне окружности с центром в точке О(0,0) и радиусом r=1 (рис. 3).
| у х рис. 1 | рис. 2 | рис. 3 |
№ 5.  Так как логарифм определён только для положительных чисел, то х+у>0 или у> –х. Последнему неравенству удовлетворяют точки, лежащие выше прямой у> –х, не включая точек самой прямой. (рис. 4).
Так как логарифм определён только для положительных чисел, то х+у>0 или у> –х. Последнему неравенству удовлетворяют точки, лежащие выше прямой у> –х, не включая точек самой прямой. (рис. 4).
№ 6.  Область определения этой функции найдём из системы
Область определения этой функции найдём из системы
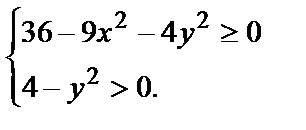
Неравенство 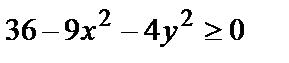 перепишем в виде
перепишем в виде  или
или  Уравнение
Уравнение  определяет точки эллипса, а неравенство
определяет точки эллипса, а неравенство  - точки, лежащие на эллипсе и внутри него.
- точки, лежащие на эллипсе и внутри него.
Неравенство 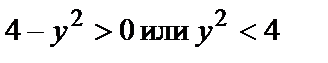 запишем в виде
запишем в виде 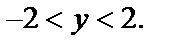 Оно определяет точки, лежащие между прямыми
Оно определяет точки, лежащие между прямыми 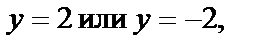 исключая точки прямых. Итак, область определения функции есть множество точек внутри эллипса между прямыми.
исключая точки прямых. Итак, область определения функции есть множество точек внутри эллипса между прямыми.
см. рис. 5.
| у 0 х y=-x рис. 4 | 3 у 2 2 0 х рис. 5 |
Если точка М0(х0,у0) лежит в области определения функции 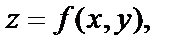 то её значение в этой точке называют частным значением функции и обозначают
то её значение в этой точке называют частным значением функции и обозначают  или
или  , или
, или 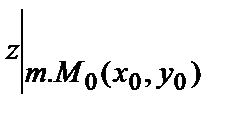 .
.
Например, для функции
 её частные значения в точках
её частные значения в точках 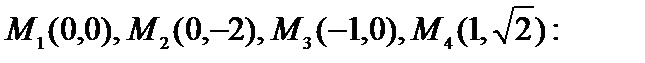

Перейдём теперь к понятию предела функции двух переменных.
Рассмотрим последовательность точек 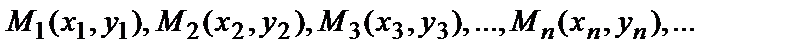 Будем говорить, что эта последовательность точек сходится к точке М0(х0,у0) (стремится к точке М0), если расстояние
Будем говорить, что эта последовательность точек сходится к точке М0(х0,у0) (стремится к точке М0), если расстояние 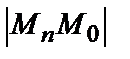 стремится к нулю при
стремится к нулю при  или если
или если  при
при 
Определение. Если для любой последовательности точек 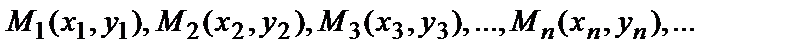 сходящейся к точке М0(х0,у0), соответствующая последовательность
сходящейся к точке М0(х0,у0), соответствующая последовательность  значений функции
значений функции  имеет пределом одно и то же число А, то это число называют пределом функции
имеет пределом одно и то же число А, то это число называют пределом функции  при
при 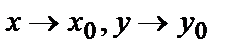 и пишут
и пишут  или
или 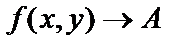 при
при 
Так например, функция 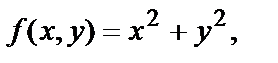 определённая на всей плоскости, имеет пределом число 5 при
определённая на всей плоскости, имеет пределом число 5 при  Действительно, для любой последовательности точек
Действительно, для любой последовательности точек  сходящейся к точке (1,2), имеем
сходящейся к точке (1,2), имеем 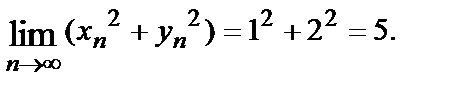
Следовательно, 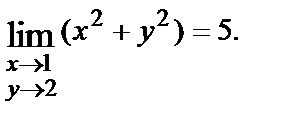
Определение. Если существует конечный  и
и  то функция
то функция  называется непрерывной в точке М0(х0,у0).
называется непрерывной в точке М0(х0,у0).
Например, функция 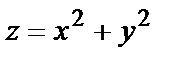 непрерывна в любой точке плоскости. Функция
непрерывна в любой точке плоскости. Функция  имеет множество точек, где она не является непрерывной. Эти точки расположены на прямой
имеет множество точек, где она не является непрерывной. Эти точки расположены на прямой  т.к. в любой точке этой прямой дробь
т.к. в любой точке этой прямой дробь  не определена. Итак, функция
не определена. Итак, функция  будем говорить, разрывна в каждой точке прямой
будем говорить, разрывна в каждой точке прямой 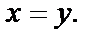 Функция
Функция  не определена в начале координат т. О(0,0) и поэтому в ней не является непрерывной. Точка О(0,0) является точкой разрыва функции
не определена в начале координат т. О(0,0) и поэтому в ней не является непрерывной. Точка О(0,0) является точкой разрыва функции 
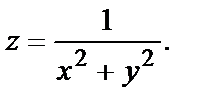
Дата добавления: 2014-12-30; просмотров: 1420;
