Приложения теории бесконечных рядов
Теория рядов применяется для решения важнейших задач математического анализа, при исследовании многих естественных и технических явлений, для описания колебательных процессов, радио- и электросигналов и т.д. Отменим некоторые из таких задач.
Прежде всего это исследование элементарных функций. Для решения задач практики очень важно уметь вычислять значения элементарных функций при любых значениях аргумента. Таблицы элементарных функций составляются с помощью теории бесконечных рядов.
Пример 1. Покажем, например, как вычислить 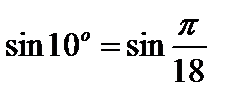 с точностью до 0,001.
с точностью до 0,001.
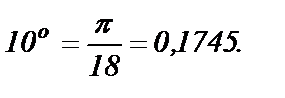
В примере 2 п. 6.10 мы получили
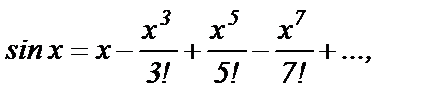
причем это равенство верно для всех 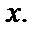 Подставим в это равенство
Подставим в это равенство 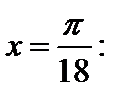
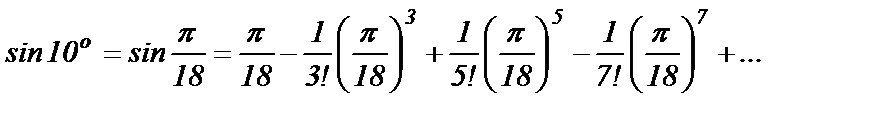
Получен знакочередующийся ряд, удовлетворяющий всем требованиям признака Лейбница. Значит, оставив для вычисления 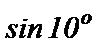 только два первых члена этого ряда, мы допустим ошибку, не превышающую третьего члена, т.е.
только два первых члена этого ряда, мы допустим ошибку, не превышающую третьего члена, т.е. 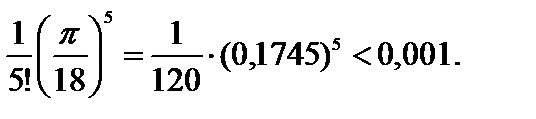
Итак, 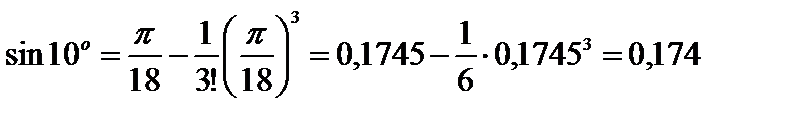
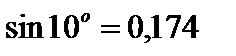 с точностью до 0,001.
с точностью до 0,001.
Пример 2. Вычислим значение числа 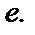 Воспользуемся разложением функции
Воспользуемся разложением функции 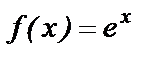 в ряд Тейлора (пример 1 п. 6.10):
в ряд Тейлора (пример 1 п. 6.10):
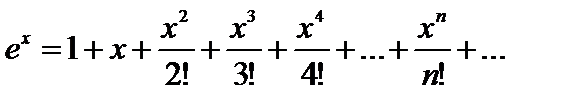 для
для 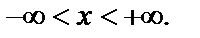
Оценим ошибку, которую мы допустим, полагая 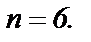 Тогда остаток ряда
Тогда остаток ряда 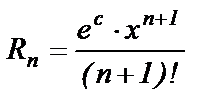 и ошибка будет меньше, чем
и ошибка будет меньше, чем 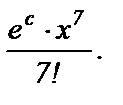
Чтобы получить число 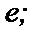 положим в ряде для
положим в ряде для 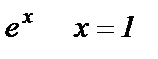 и
и 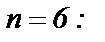
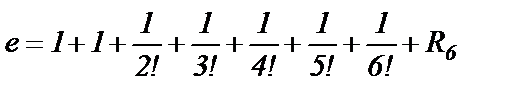 или
или
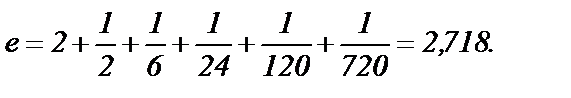
Допущена ошибка 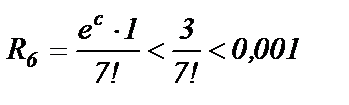
Итак, 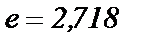 с точностью до
с точностью до 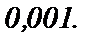
Бесконечные ряды применяются также для вычисления интегралов, которые не выражаются через элементарные функции. Покажем это на примере.
Пример 3. Пусть требуется вычислить интеграл 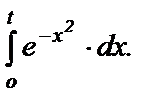
Воспользуемся рядом Тейлора для 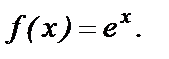
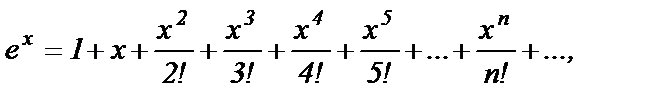 где
где 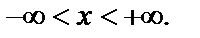
Заменим 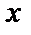 на
на 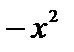 и проинтегрируем обе части полученного равенства:
и проинтегрируем обе части полученного равенства:
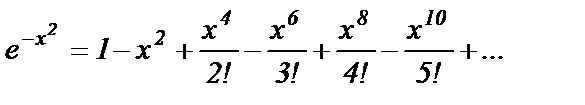
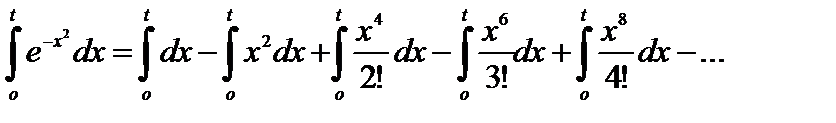 или
или
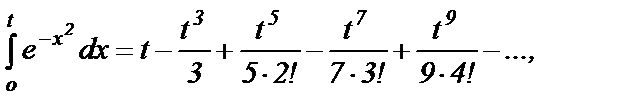 где
где 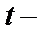 любое число.
любое число.
С помощью полученного равенства можно при всяком значении 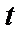 вычислить с любой степенью точности
вычислить с любой степенью точности 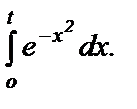 Так и составлены таблицы значений этого интеграла.
Так и составлены таблицы значений этого интеграла.
Так же получены таблицы значений еще одного, не выражающегося в элементарных функциях, интеграла 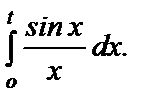
Покажем, что с помощью теории рядов обнаруживается глубокая связь между показательной функцией 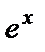 и тригонометрическими функциями
и тригонометрическими функциями 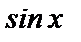 и
и 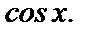
Уже внешний вид рядов Тейлора для этих функций наталкивает на мысль о существовании некоторой зависимости между ними. Для любого действительного 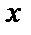 имеем:
имеем:
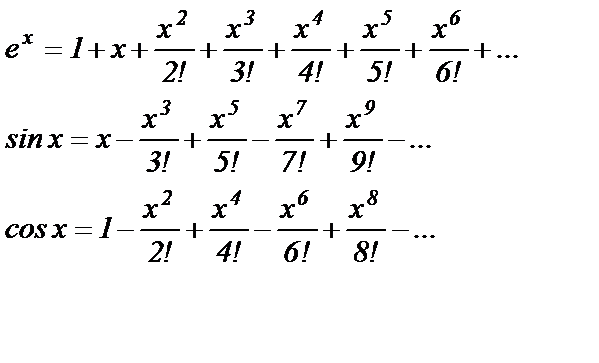
До сих пор мы говорили о действительных функциях действительного аргумента, т.е. и 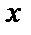 и
и 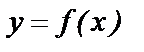 были действительными числами. Будем считать, что функции
были действительными числами. Будем считать, что функции 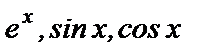 могут быть определены и для комплексных чисел. Понятно, что рассуждения эти не являются строгими. Мы только поясняем существо вопроса.
могут быть определены и для комплексных чисел. Понятно, что рассуждения эти не являются строгими. Мы только поясняем существо вопроса.
Итак, в ряд Тейлора для 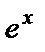 вместо переменной
вместо переменной 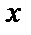 подставим мнимое число
подставим мнимое число
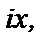 учтем что
учтем что
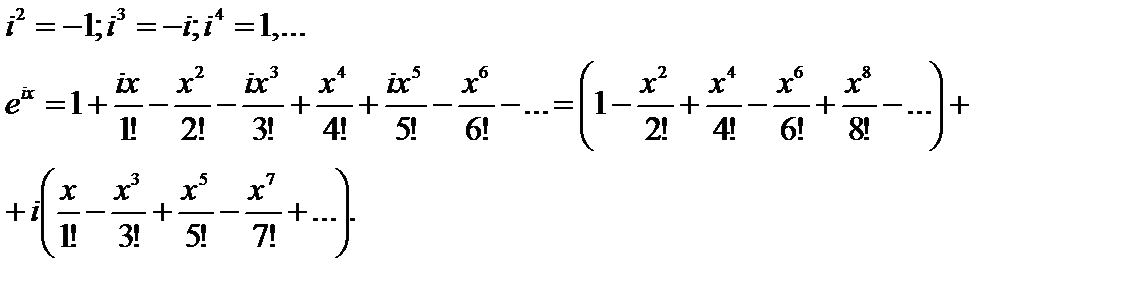
Получили равенство 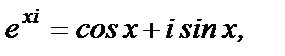 называемое формулой Эйлера. Эта формула выведена в ХVIII веке петербургским академиком Леонардом Эйлером.
называемое формулой Эйлера. Эта формула выведена в ХVIII веке петербургским академиком Леонардом Эйлером.
Вопросы для самоконтроля
Прежде чем Вы приступите к выполнению контрольного задания, попробуйте ответить на следующие вопросы. В конце каждого вопроса указан пункт настоящего курса, в котором Вы сможете найти ответ на поставленный вопрос.
Предлагаемые вопросы:
1. Какая последовательность называется арифметической? Как записать формулу ее общего члена и формулу суммы 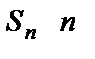 ее первых членов? (п. 6.3)
ее первых членов? (п. 6.3)
2. Какая последовательность называется геометрической? Как записать формулу ее общего члена и формулу суммы 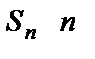 ее первых членов? (п. 6.3)
ее первых членов? (п. 6.3)
3. Что называется бесконечным числовым рядом? Как можно коротко записать ряд? (п. 6.4)
4. Дать определение сходящегося (расходящегося) числового ряда. (п. 6.4)
5. Как сформулировать необходимый признак сходимости ряда? Что
можно сказать о ряде, для которого не выполняется этот признак? (п. 6.4)
6. Как сформулировать признак сравнения для знакоположительных
рядов? (п. 6.5)
7. Привести примеры числовых рядов, которые часто используются для сравнения (гармонический ряд, ряд геометрической прогрессии).
(пример 3 п. 6.4; пример 10 п. 6.5).
8. Как сформулировать признак Даламбера? (п. 6.5)
9. Как сформулировать интегральный признак Коши? (п. 6.5)
10. Для исследования каких рядов используется признак Лейбница?
Как он формулируется? Что можно сказать о ряде, для которого не
выполняется хотя бы одно условие признака Лейбница? (п. 6.6)
11. Дать определение сходящегося абсолютно и сходящегося условно знакопеременного ряда. (п. 6.7)
12. Что называется функциональным рядом и областью его сходимости? (п. 6.8)
13. Записать степенной ряд 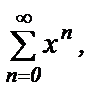 указать область сходимости и сумму этого ряда. (п. 6.9)
указать область сходимости и сумму этого ряда. (п. 6.9)
14. Какими свойствами обладают степенные ряды? (п. 6.9)
15. Какую функцию можно представить в виде ряда Тейлора? В какой области этот ряд сходится к данной функции? Как найти эту область? (п. 6.10)
Бесконечные ряды являются важнейшим аппаратом для исследования функций, вычисления значений функций, приближенного вычисления определенных интегралов, приближенного решения дифференциальных уравнений и т.д.
Вы должны уметь пользоваться основными разложениями в степенной ряд функций 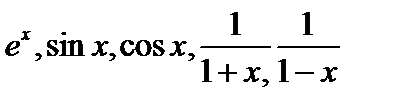 для получения разложений в ряд функций
для получения разложений в ряд функций 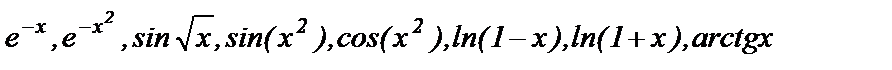 и интегралов
и интегралов 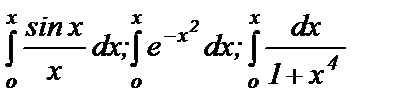 и т.д.
и т.д.
Много таких примеров рассмотрено в п. 6.9, 6.10, 6.11 настоящего курса.
Приведем, наконец, пример решения контрольного задания, которое содержит задачи №№ 1-9. Задачи № 1 и № 2 не требуют подробного рассмотрения.
Дата добавления: 2014-12-30; просмотров: 1354;
