Частные производные функции нескольких переменных
Пусть в некоторой области дана функция 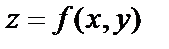 и точка М(х,у) – произвольная точка этой области. Дадим независимой переменной х приращение
и точка М(х,у) – произвольная точка этой области. Дадим независимой переменной х приращение 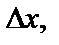 оставляя значение переменной у неизменным.
оставляя значение переменной у неизменным.
При этом функция z получит приращение 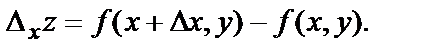
Оно называется частным приращением этой функции по переменной х и характеризует изменение функции 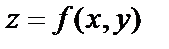 при изменении только аргумента х. Отношение
при изменении только аргумента х. Отношение 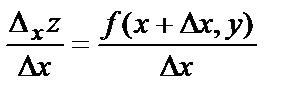 равно средней скорости изменения функции на участке от точки М(х,у) до точки
равно средней скорости изменения функции на участке от точки М(х,у) до точки 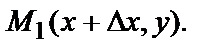
Определение. Предел отношения 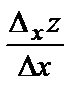 при
при 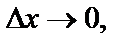 если он существует и конечен, называется частной производной функции
если он существует и конечен, называется частной производной функции 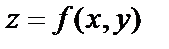 по переменной х в точке (х,у).
по переменной х в точке (х,у).
Частную производную по х от функции 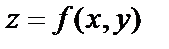 обозначают следующими символами:
обозначают следующими символами: 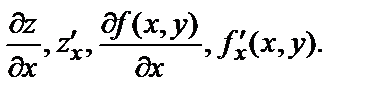
Таким образом, 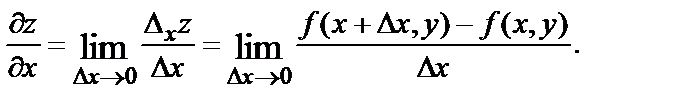
Этот предел характеризует скорость изменения функции по х в точке М(х,у). Таков физический смысл частной производной.
Легко видеть полную аналогию с определением производной для функции 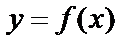 одной переменной и её физическим смыслом.
одной переменной и её физическим смыслом.
Аналогично, считая х неизменной и давая переменной у приращение 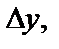 получим частное приращение функции
получим частное приращение функции 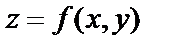 по у:
по у: 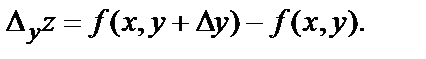
Определение. Предел отношения 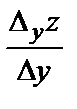 при
при 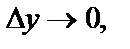 если он существует и конечен, называется частной производной функции
если он существует и конечен, называется частной производной функции 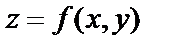 по переменной у в точке (х,у).
по переменной у в точке (х,у).
Частная производная по у обозначается одним из символов: 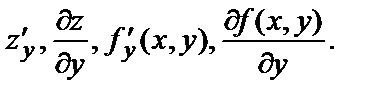
Таким образом, 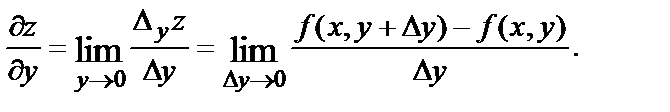
Эта частная производная численно равна скорости изменения по у функции 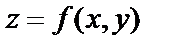 в точке М(х,у).
в точке М(х,у).
Значения частных производных 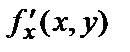 и
и 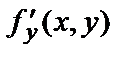 зависят от координат х, у рассматриваемой точки М, т.е. в свою очередь являются функциями двух переменных.
зависят от координат х, у рассматриваемой точки М, т.е. в свою очередь являются функциями двух переменных.
Вычисление частных производных по х (или по у) от конкретных функций производится по известным для функции одной переменной правилам. А именно, для вычисления частной производной по х следует считать у постоянной величиной и пользоваться уже известными правилами и формулами дифференцирования. Для вычисления частной производной по у следует считать х постоянной величиной и только у – независимой переменной.
Например, для функции 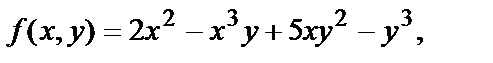 полагая у постоянной, получим
полагая у постоянной, получим 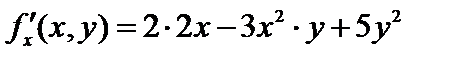
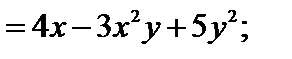 полагая х постоянной, получим
полагая х постоянной, получим 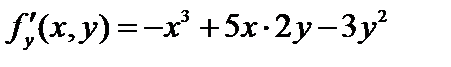
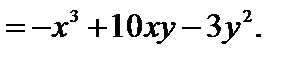 В частности, значение найденных частных производных в точке М0(-1,2):
В частности, значение найденных частных производных в точке М0(-1,2):
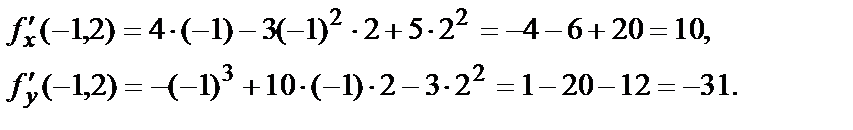
Частные производные функции двух переменных имеют простой геометрический смысл.
Вспомним вначале определение и геометрический смысл производной функции одной переменной. Для функции 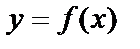 производной в точке х называется
производной в точке х называется 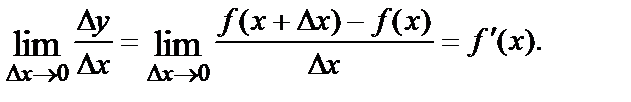 Графиком функции
Графиком функции 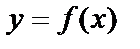 является некоторая линия на плоскости. Значение производной в точке х0 равно угловому коэффициенту (тангенсу угла наклона) касательной, проведённой к графику функции в точке, где х=х0, т.е.
является некоторая линия на плоскости. Значение производной в точке х0 равно угловому коэффициенту (тангенсу угла наклона) касательной, проведённой к графику функции в точке, где х=х0, т.е. 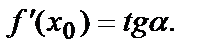
| у у=f(x) y0 М0 a 0 x0 х |
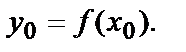
По определению частная производная функции двух переменных по х 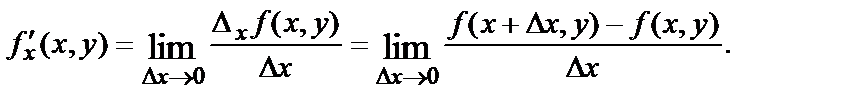
Геометрически уравнение 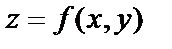 задает в пространстве некоторую поверхность. При вычислении частной производной этой функции по х в точке М0(х0,y0) мы полагаем y=y0. В сечении поверхности
задает в пространстве некоторую поверхность. При вычислении частной производной этой функции по х в точке М0(х0,y0) мы полагаем y=y0. В сечении поверхности 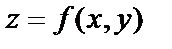 плоскостью
плоскостью 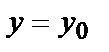 получаем линию, которая проходит через точку
получаем линию, которая проходит через точку 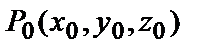 поверхности (для неё
поверхности (для неё 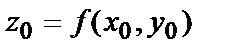 ). Значение частной производной по
). Значение частной производной по 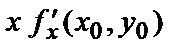 равно тангенсу угла, который касательная к полученной линии в точке
равно тангенсу угла, который касательная к полученной линии в точке 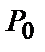 образует с осью Ох (или с прямой, ей параллельной).
образует с осью Ох (или с прямой, ей параллельной).

Для функции трёх переменных 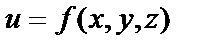 определение частных производных даётся также, как и для функции двух переменных:
определение частных производных даётся также, как и для функции двух переменных:
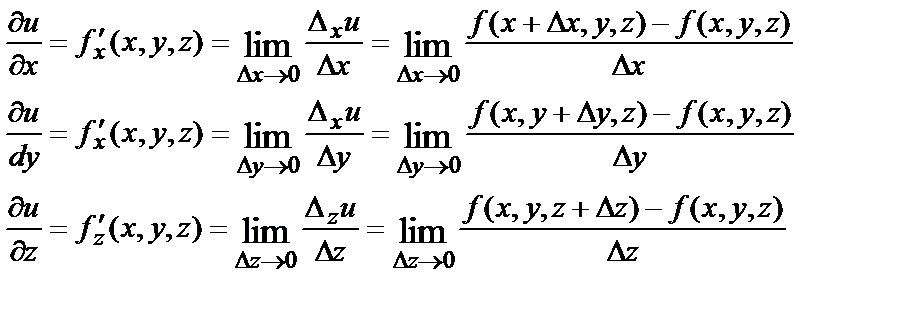
Рассмотрим несколько примеров.
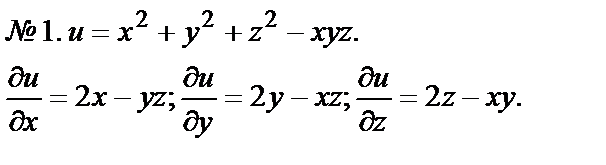
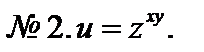 При отыскании
При отыскании 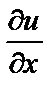 полагаем z и y постоянными и применяем формулу
полагаем z и y постоянными и применяем формулу 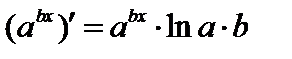
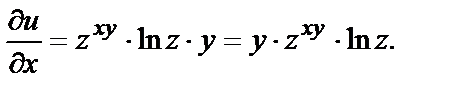
Аналогично, 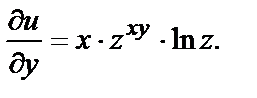
При отыскании 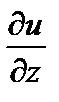 полагаем x и у постоянными, тогда
полагаем x и у постоянными, тогда 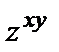 - степенная функция и
- степенная функция и 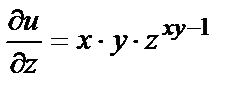
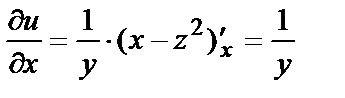 (Здесь множитель
(Здесь множитель 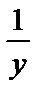 выносится как постоянный).
выносится как постоянный).

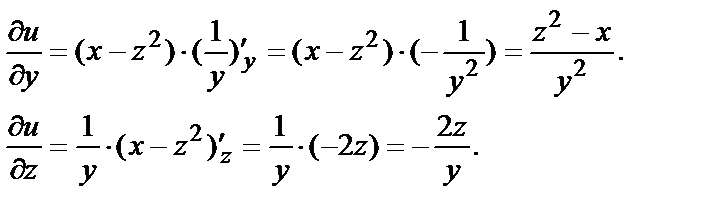
Мы рассматривали частные приращения функции 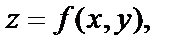 полученные ею в результате изменения только одной независимой переменной. Если изменяются обе переменные, то полученное приращение функции называется полным приращением и обозначается
полученные ею в результате изменения только одной независимой переменной. Если изменяются обе переменные, то полученное приращение функции называется полным приращением и обозначается 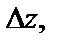 т.е.
т.е.
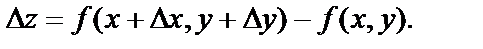
Определение. Функция 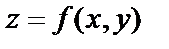 называется дифференцируемой в точке М(х,у), если её полное приращение в этой точке можно представить в виде:
называется дифференцируемой в точке М(х,у), если её полное приращение в этой точке можно представить в виде:
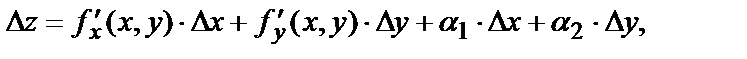 где
где 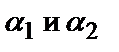 — бесконечно малые при
— бесконечно малые при 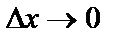 и
и 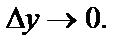 При этом слагаемое
При этом слагаемое 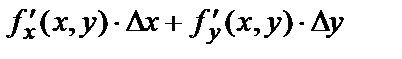 называется полным дифференциалом функции в точке М(х,у) и является главной частью полного приращения. На самом деле, при
называется полным дифференциалом функции в точке М(х,у) и является главной частью полного приращения. На самом деле, при 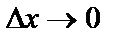 и
и 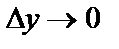 полный дифференциал функции отличается от её полного приращения на величину
полный дифференциал функции отличается от её полного приращения на величину 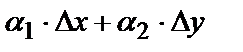 бесконечно малую более высокого порядка, чем
бесконечно малую более высокого порядка, чем 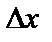 и
и 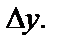
Полный дифференциал функции 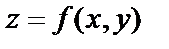 обозначают символом
обозначают символом 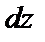 или
или 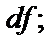 следовательно, формула полного дифференциала:
следовательно, формула полного дифференциала:
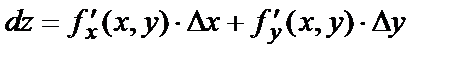 или
или
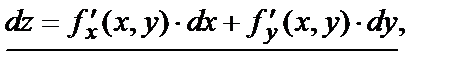 где
где 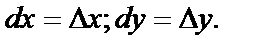
В задачах приближенного вычисления часто полное приращение функции заменяют её полным дифференциалом, т.е. полагают 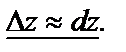 И это приближенное равенство тем точнее, чем меньше приращения
И это приближенное равенство тем точнее, чем меньше приращения 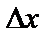 и
и 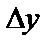 независимых переменных.
независимых переменных.
По аналогии для функции 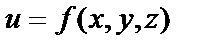 формула полного дифференциала имеет вид:
формула полного дифференциала имеет вид:
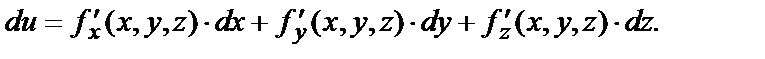
№ 3. Найти полный дифференциал функции 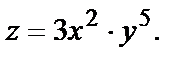
Формула полного дифференциала 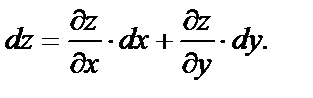
Найдём частные производные:
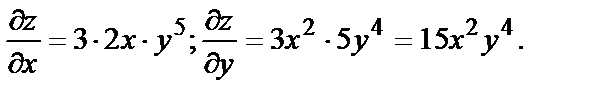
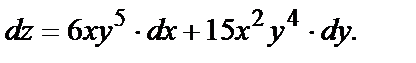
№ 4. Вычислить значение полного дифференциала функции 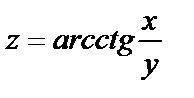 в точке (1,3) при заданных приращениях
в точке (1,3) при заданных приращениях 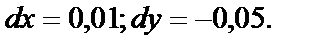
Используем формулу 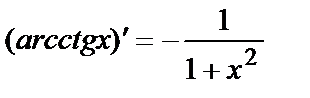 и найдём частные производные:
и найдём частные производные:
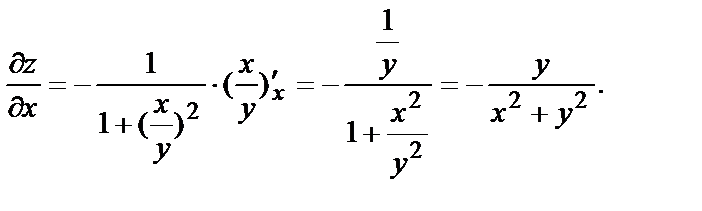
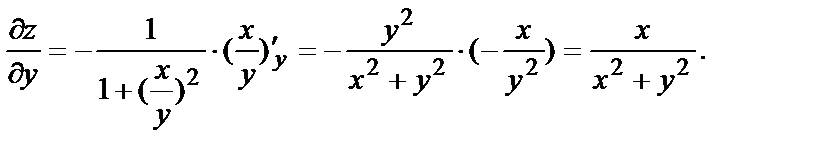
Вычислим их значения при х=1, у=3.
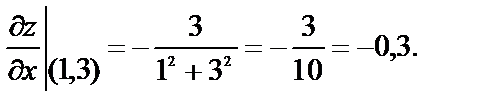
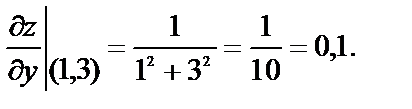
Подставим в формулу полного дифференциала 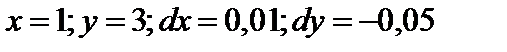 и получим его значение:
и получим его значение:
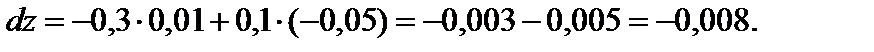
№ 5. Найти формулу полного дифференциала функции 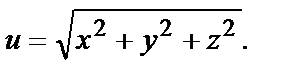
Найдём частные производные по всем трём независимым переменным:
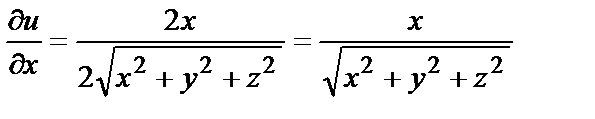
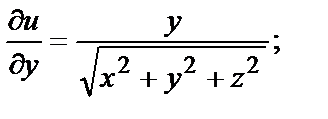
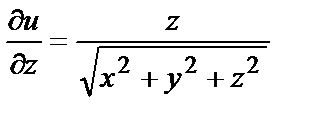 и подставим в формулу:
и подставим в формулу:
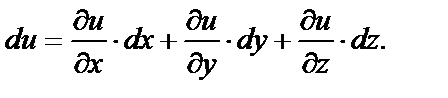
Получим 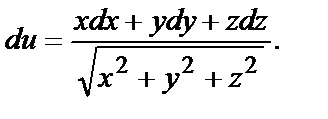
Дата добавления: 2014-12-30; просмотров: 2085;
