Экстремумы функции двух переменных
Теория экстремумов функций двух переменных во многом аналогична соответствующей теории для функций одного переменного.
Определение. Назовём d - окрестностью (дельта - окрестностью) точки М0 множество всех точек М, лежащих внутри круга радиуса d с центром в точке М0.
Пусть дана функция 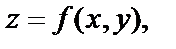 определённая в некоторой области D, М0(х0,у0) – точка внутри этой области.
определённая в некоторой области D, М0(х0,у0) – точка внутри этой области.
Определение. Точка М0(х0,у0) называется точкой максимума функции 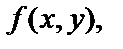 если в области D существует такая окрестность точки М0(х0,у0), что для всех точек М(х,у) этой окрестности
если в области D существует такая окрестность точки М0(х0,у0), что для всех точек М(х,у) этой окрестности 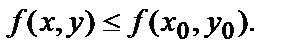
Замечая, что приращение функции 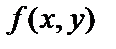 в точке (х0,у0)
в точке (х0,у0)
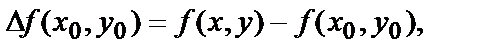
можно записать, что в точке максимума 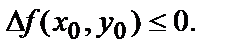

Аналогично точка М0(х0,у0) называется точкой минимума функции 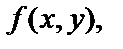 если в некоторой точке окрестности этой точки
если в некоторой точке окрестности этой точки 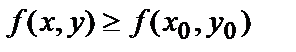 или
или 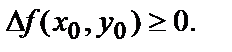

Если М0 – точка максимума функции 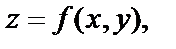 то значение функции в этой точке
то значение функции в этой точке 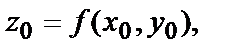 называют максимальным значением функции. Если точка М0 – точка минимума,то
называют максимальным значением функции. Если точка М0 – точка минимума,то 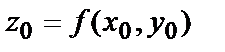 - минимальное значениефункции.
- минимальное значениефункции.
Точки минимума и максимума называют точками экстремума функции, а значения в этих точках экстремумами этой функции.
Понятия экстремумов носят локальный характер: значения функции в точке М0(х0,у0) сравнивают со значениями функции в достаточно близких точках.
В данной области функция может не иметь экстремумов, а может иметь несколько минимумов или несколько максимумов.
При этом некоторые минимумы могут оказаться больше какого-то максимума. Не следует смешивать экстремумы функции с её наименьшими значениями в данной области. Позже рассмотрим подробно эту задачу.
Рассмотрим примеры.
№ 1. Функция 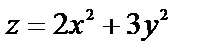 в точке О(0,0) имеет минимум, так как
в точке О(0,0) имеет минимум, так как 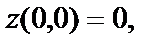 а в любой другой точке
а в любой другой точке 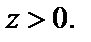
№ 2.  Эта функция в точке О(0,0) имеет максимум, так как
Эта функция в точке О(0,0) имеет максимум, так как 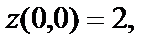 а в любой другой точке
а в любой другой точке 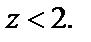
№ 3. 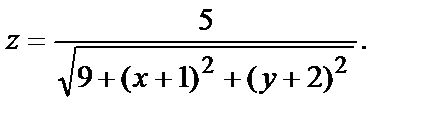 Для этой функции точка М0(-1,-2) – точка максимума, так как в этой точке
Для этой функции точка М0(-1,-2) – точка максимума, так как в этой точке 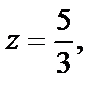 а в любой другой точке значение функции
а в любой другой точке значение функции 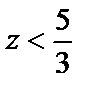 (знаменатель дроби увеличивается).
(знаменатель дроби увеличивается).
№ 4. Легко видеть, что функция 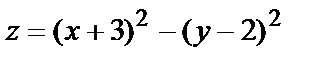 в точке М0(-3,2) не имеет экстремума. Значение в этой точке
в точке М0(-3,2) не имеет экстремума. Значение в этой точке 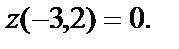 Рассмотрим любые точки М(х,2). При любом х, как угодно близком к –3, значение
Рассмотрим любые точки М(х,2). При любом х, как угодно близком к –3, значение 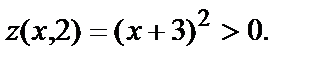 Для точек М(-3,у) при любом у, как угодно близком к 2, значение
Для точек М(-3,у) при любом у, как угодно близком к 2, значение 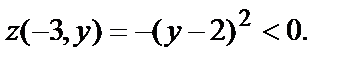 Таким образом, в любой окрестности точки М0(-3,2) найдутся точки, в которых значение функции больше значения в точке М0, и найдутся точки, в которых значение меньше значения в точке М0.
Таким образом, в любой окрестности точки М0(-3,2) найдутся точки, в которых значение функции больше значения в точке М0, и найдутся точки, в которых значение меньше значения в точке М0.
Приведённые примеры были очень простыми. В более сложных случаях нужны специальные методы разыскания экстремальных точек. Эти методы очень похожи на исследование функции одной переменной на экстремум.
Рассмотрим функцию 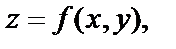 которая в области D имеет непрерывные первые частные производные.
которая в области D имеет непрерывные первые частные производные.
Необходимые условия существования экстремума: если функция 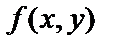 в точке (х0,у0) имеет экстремум, то
в точке (х0,у0) имеет экстремум, то 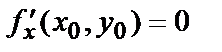 и
и 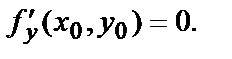
В примере № 1 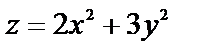 точка О(0,0) – точка минимума. В этой точке
точка О(0,0) – точка минимума. В этой точке 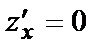 и
и 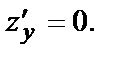
В примере № 2  точка О(0,0) – точка максимума. Найдём производные этой функции и вычислим их в точке О(0,0).
точка О(0,0) – точка максимума. Найдём производные этой функции и вычислим их в точке О(0,0).
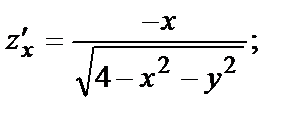
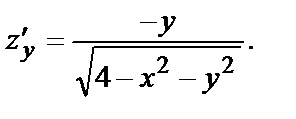
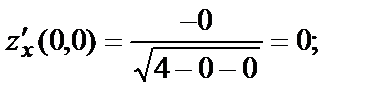
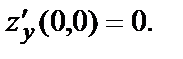
В примере № 3 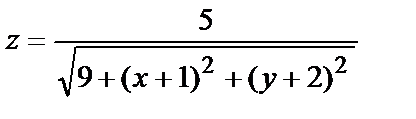 . М0(-1,-2) – точка максимума. Найдём частные производные функции.
. М0(-1,-2) – точка максимума. Найдём частные производные функции.
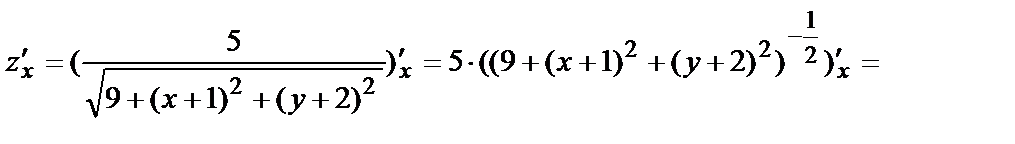
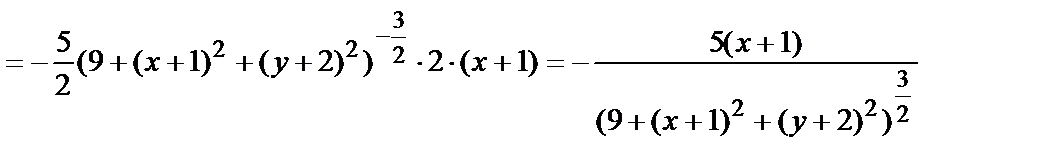
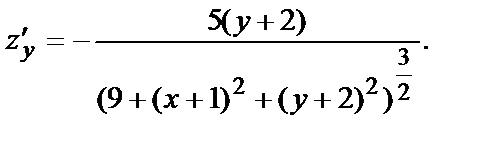
Очевидно, в точке М0(-1,-2) обе частные производные равны нулю.
Итак, действительно, в точке экстремума функции обе её частные производные равны нулю.
Будем называть критическими точками функции те её точки, где обе частные производные равны нулю. Точки экстремума функции являются её критическими точками. Но не всякая критическая точка функции будет её точкой экстремума.
Например, для функции 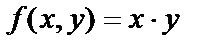 частные производные
частные производные 
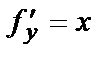 обращаются в нуль при
обращаются в нуль при  т.е. точка О(0,0) – критическая точка для функции
т.е. точка О(0,0) – критическая точка для функции  Но в этой точке нет ни максимума, ни минимума, так как вблизи точки О(0,0) найдутся точки, где значение функции будет и больше и меньше значения
Но в этой точке нет ни максимума, ни минимума, так как вблизи точки О(0,0) найдутся точки, где значение функции будет и больше и меньше значения 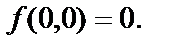
Действительно, если точка М(х,у) лежит в I четверти или в III четверти, то 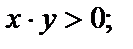 если же точка М(х,у) лежит во II или в IV координатных углах,
если же точка М(х,у) лежит во II или в IV координатных углах, 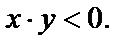
Поэтому равенство нулю частных производных – только необходимое условие существования экстремума. Оно не является достаточным.
Найдя критические точки функции, для чего надо решить систему уравнений
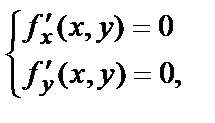
следует при помощи некоторых достаточных условий выделить те точки, где существует экстремум.
Для этого рассмотрим выражение
 состоящее из вторых частных производных функции.
состоящее из вторых частных производных функции.
Достаточные условия экстремума: если точка М0(х0,у0) – критическая точка функции и
1) если 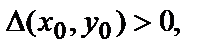 то в точке (х0,у0) функция
то в точке (х0,у0) функция 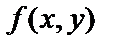 имеет экстремум, а именно:
имеет экстремум, а именно:
при 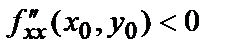 - максимум,
- максимум,
при 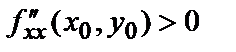 - минимум;
- минимум;
2) если 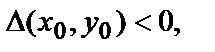 то в точке (х0,у0) функция
то в точке (х0,у0) функция 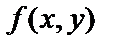 экстремума не имеет;
экстремума не имеет;
3) если 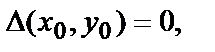 то нужны дополнительные исследования.
то нужны дополнительные исследования.
Пример № 5. Найти экстремумы функции 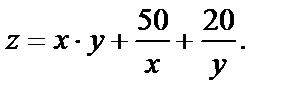
Эта функция определена всюду, кроме точек, где 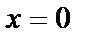 и
и  (кроме точек, лежащих на осях координат).
(кроме точек, лежащих на осях координат).
Найдём все частные производные, нужные для исследования.
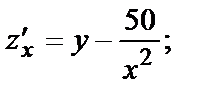
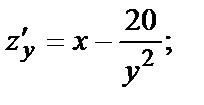
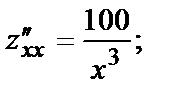
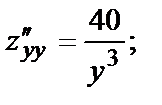
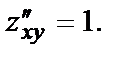
Найдём критические точки функции, решив систему
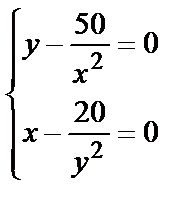 или
или 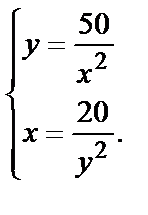
Разделив второе уравнение на первое, получим
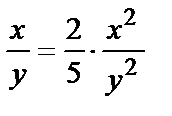 или
или 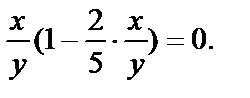
Так как 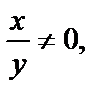 то
то 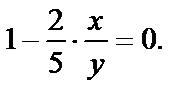
Отсюда 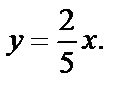 Подставим в первое уравнение системы:
Подставим в первое уравнение системы: 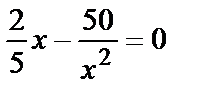 или
или 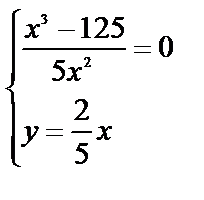
Получим 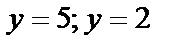 - координаты критической точки.
- координаты критической точки.
Вычислим в полученной критической точке М(5,2) значения вторых частных производных:
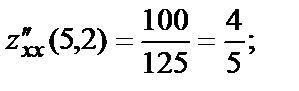
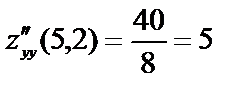 .
.
Найдём значение выражения
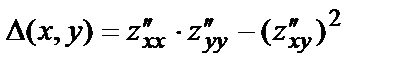 в точке М0(5,2).
в точке М0(5,2).
 что означает, что в точке М0(5,2) есть экстремум, а именно минимум, так как
что означает, что в точке М0(5,2) есть экстремум, а именно минимум, так как 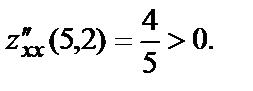 Остаётся найти значение функции
Остаётся найти значение функции  - минимальное значение функции.
- минимальное значение функции.
Пример № 6. Исследовать на экстремум функцию 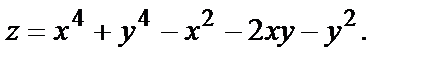
Эта функция определена при любых  Найдём все производные первого и второго порядка:
Найдём все производные первого и второго порядка:
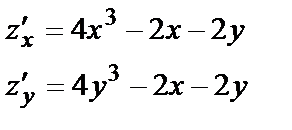
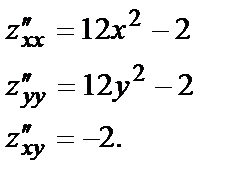
Решив систему 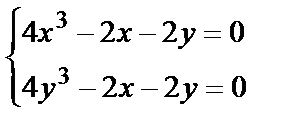 , найдём критические точки. Так как
, найдём критические точки. Так как 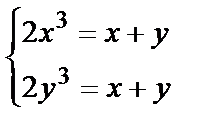 , то равны левые части уравнений
, то равны левые части уравнений 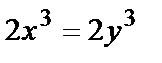 или
или 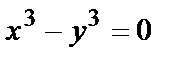
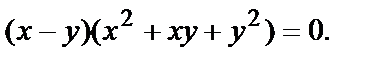 Отсюда
Отсюда 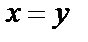 . Подставим в первое уравнение y=x:
. Подставим в первое уравнение y=x: 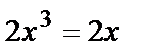 или
или
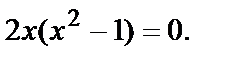
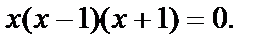
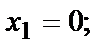
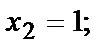
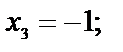
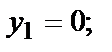
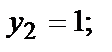
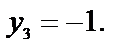
Получим три критические точки М1(0,0); М2(1,1); М3(-1,-1).
Найдём значение выражения 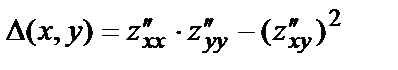 в каждой критической точке.
в каждой критической точке.
В точке М1(0,0): 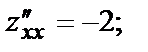
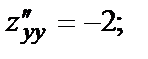
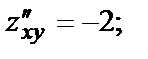
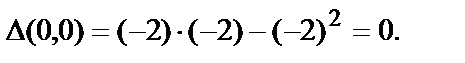
В точке В точке М1(0,0) вопрос об экстремуме остаётся открытым.
В точке М2(1,1): 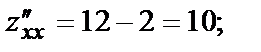
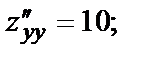
 что означает, что в точке М2(1,1) функция имеет экстремум, а именно минимум, т.к.
что означает, что в точке М2(1,1) функция имеет экстремум, а именно минимум, т.к.
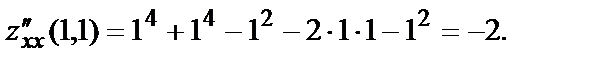
В точке М3(-1,-1): 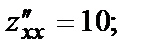
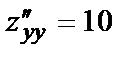 и
и
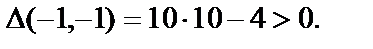 А так как
А так как 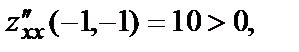 точка М3(-1,-1) – точка минимума. Значение функции в этой точке
точка М3(-1,-1) – точка минимума. Значение функции в этой точке 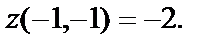
Итак, функция 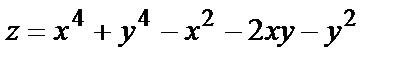 имеет два минимума в точках М2(1,1) и М3(-1,-1) величиной
имеет два минимума в точках М2(1,1) и М3(-1,-1) величиной 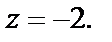
Дата добавления: 2014-12-30; просмотров: 2019;
