Задача № 2. Найти точки разрыва функции и построить график
Найти точки разрыва функции и построить график
Функция ƒ(х) определена для всех действительных х и непрерывна на каждом из указанных промежутков: (–∞; –1), [–1; 0], (0, +∞). Исследуем функцию ƒ(х) на непрерывность в точках х= –1 и х=0.
Для этого в каждой из этих точек найдем односторонние пределы.
Так как односторонние пределы различны, то х= –1 – точка разрыва первого рода.
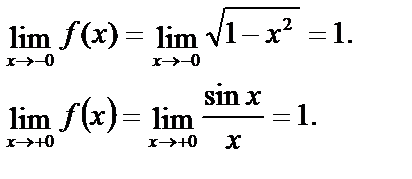
Односторонние пределы равны, т. е. в точке х=0 существует предел функции и 
Сравним этот предел со значением функции в точке: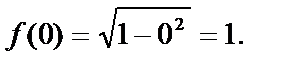 
Так как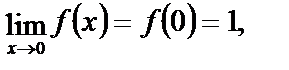 
то в точке х=0 функция ƒ(х) непрерывна.
Построим график функции ƒ(х), учитывая, что
1) 
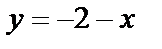– уравнение прямой,
2) 
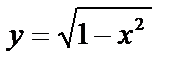– уравнение верхней полуокружности 
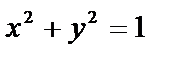с центром в начале координат и радиусом, равным единице, а при условии –1 £ х £ 0 уравнение 
определяет четверть окружности.
3) для х > 0 график задается уравнением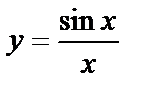 
. Точки пересечения этой кривой с осью Ох найдем из уравнения 
при х > 0. х=πn, где n=1, 2, 3, 4, …
Рис. 26.
Дата добавления: 2014-12-30; просмотров: 913;