Задача № 4. Составить уравнения касательных к линии в точках, где х=0 и х=4

Составить уравнения касательных к линии 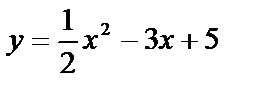в точках, где х=0 и х=4. Найти точку пересечения касательных и угол между ними. Сделать чертеж.

Уравнение касательной к линии у=ƒ(х) имеет вид

,

где у₀=ƒ(х₀).

В точке х=0 у(0)=ƒ(0)=5.

у¢=ƒ¢(х)=х–3 ƒ¢(0)= –3.

Уравнение касательной в точке М₁(0, 5) имеет вид у–5= –3(х–0) или

у= –3х+5.

В точке х=4 у(4)=ƒ(4)=1. ƒ¢(4)=4–3=1.

Уравнение касательной в точке М₂(4, 1) имеет вид у–1=х–4 или

у=х–3.

Точку пересечения касательных получим, решив систему

Точка пересечения М₃(2, –1).

Угол φ между касательными найдем из формулы:

,

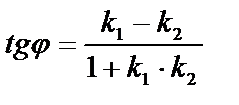где k₁= –3; k₂=1 – угловые коэффициенты касательных.

.

Угол φ=arctg 2.

Построим данную линию 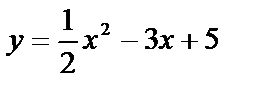– параболу с вершиной в точке, где х=3, т. к. у¢=0 при х=3. Найдем .

Точка М₄(3; ) – вершина параболы.

Рис. 27.