Дифференциал функции. Пусть функция у=ƒ(х) определена на множества Х и дифференцируема в каждой его точке.

Пусть функция у=ƒ(х) определена на множества Х и дифференцируема в каждой его точке.

Определение. Дифференциалом функции называется произведение

производной функции на приращение аргумента и

обозначается dy или dƒ(х), т. е.

dy=ƒ¢(x)·Δx

Пусть дана функция у=х. Тогда у¢=1. Дифференциал этой функции dy=1·Δx, т.е. dx=Δx.

Поэтому формулу дифференциала записывают в виде

dy=f¢(x)·dx

Отсюда 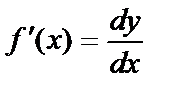, т. е. производная есть отношение дифференциалов функции и аргумента. Иногда удобно пользоваться именно таким «определением» производной.