Пример 11. Дана кривая . Составить уравнения касательных к этой кривой, параллельных
Дана кривая 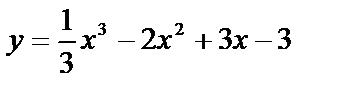 . Составить уравнения касательных к этой кривой, параллельных
. Составить уравнения касательных к этой кривой, параллельных
а) оси Ох, б) прямой3х–у–5=0.
Найдем производную от у:
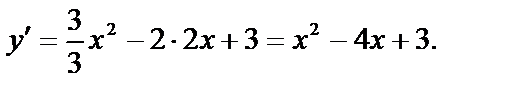
а) Если касательная параллельна оси Ох, то угловой коэффициент ее равен нулю, т. е. производная в точке х0 должна быть равна нулю: х2–4х+3=0. Решая это уравнение, находим х1=3 и х2=1. Найдем соответствующие им значения функции:
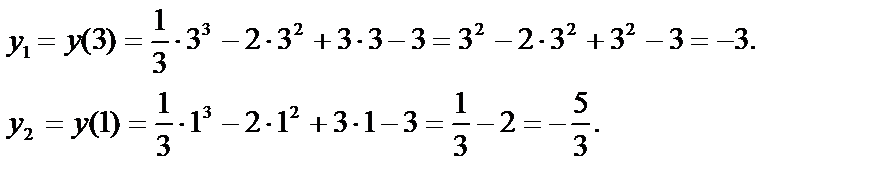
Получены две точки на данной кривой: М1(3, –3) и М2(1, 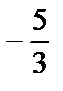 ).
).
Касательные – прямые, проходящие параллельно оси Ох, имеют уравнения: у= –3 и у= 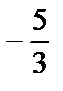 .
.
б) Если касательная параллельна прямой 3х-у-5=0, то ее угловой коэффициент равен угловому коэффициенту данной прямой:
3х–у–5=0 или у=3х–5.
k=3.
Производная у¢ в точке х0 должна быть равна 3.
х2–4х+3=3. Решая это уравнение х2–4х=0, находим х1=0 и х2=4.
Найдем соответствующие им значения функции:
у1=у(0)= –3. у2=у(4)= 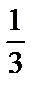 ·43–2·42+3·4–3= –
·43–2·42+3·4–3= – 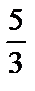 .
.
Уравнение касательной в точке М1(0,–3):
у+3=3·(х–0) или 3х–у–3=0.
Уравнение касательной в точке М2(4, – 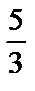 ):
):
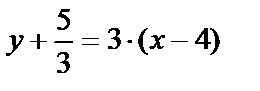 или 9х–3у–41=0.
или 9х–3у–41=0.
Дата добавления: 2014-12-30; просмотров: 2961;
