МЕТОД ДЕЛИТЕЛЬНЫХ СЕТОК

Исследования пластических деформаций при разрушении материа­лов методом делительных сеток показывают влияние концентрации напряжений (отверстий и целевых надрезов) на прочность деталей из конструкционных материалов и рассмотрены технологические задачи деформирования тонкостенных деталей из алюминиевых сплавов. Развитие техники нанесения микросеток позволило исследовать упругопластические деформации в области зарождения трещин при циклическом нагружении опорных конструкций. Исключительно эффективным оказалось приложение метода делительных сеток к задачам пластического деформирования металлов при обработке давлением. Метод оказал значительное влияние на проектирование нового инструмента и режимов штамповки, прессования, вытяжки, прокатки и тд. Современные технологические методы повышения усталостной прочности и вязкости разрушения (трещиностойкости) полуфабрикатов из штампованных заготовок и проката опираются на экспериментальные исследования, выполняемые методом делительных сеток и другими оптико-геометрическими методами.

Другое направление исследований — это изучение НДС в упругой области на резиновых и полимерных моделях при малых и больших деформациях (до 18 %). Основные зависимости метода подробно изложены в литературе, где приведены расчетные формулы и геометрические соотноше­ния в базовом элементе, поэтому только проиллюстрируем применение метода характерными задачами. Пусть в плоскости симметрии пластически деформи­руемой цилиндрической заготовки размещены ортогональные сетки с перфори­рованными отверстиями, центры которых совпадают с угловыми точками квад­рата. Будем считать материал заготовки изотропным, несжимаемым, а дефор­мации в пределах ячейки сетки однородными, причем вычисляемые компонен­ты деформаций отнесем к центру ячейки, считая их средними между базовыми точками.

Рассмотрим осесимметричную объемную задачу с тремя плоскостями симметрии, например конечные формоизменения при штамповке цилиндричес­кой поковки с прямой горизонтальной осью (рис. 7.1). В методе сеток, когда размечены базовые элементы, удобно использовать главные деформации в логарифмической форме. Окружности сетки в плоскостях симметрии штамповки после деформирования преобразуются в эллипсы с осями по главным направлениям, поэтому:

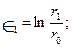
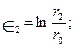
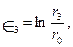(7.1)

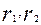где: и 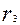- полуоси эллипсов; 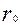— радиусы исходных окружностей сетки.

В случае деформирования тел вращения по оси z главные деформации в плоскости сетки определяются теми же зависимостями (7.1), но окружная деформация в меридиональном сечении.

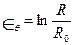, (7.2)

где: 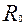и 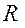— расстояния от оси симметрии z до рассматриваемой точки соот­ветственно до и после деформирования.

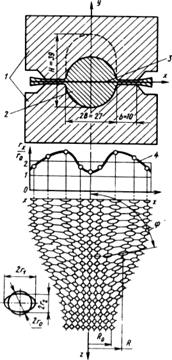
Рис. 7.1. Схема штампа с цилиндрической поковкой и сетка в плоскости заусенца после деформировании:

1 — штамп; 2 — поковка с исходной высотой Н (мм);

3 — плоскость сетки; 4 - зависимость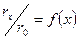

в сечении « xx » (исходная длина поковки 2l = 100 мм).

Для вычисления осевой и радиальной логарифмической деформации используют зависи мости

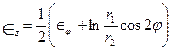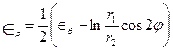, , (7.3)

где: φ находят экспериментально замером угла между направлением большой полуоси эллипса и осью z заготовки.

Эксперимент был проведен на четырех образцах из свинца: одного цельного монолитного и трех раз­резанных во взаимно перпендикулярных плоскостях симметрии. В разъемы этих образцов для качественного исследования течения металла в штампе вставляли координатные сетки из тонкой фольги с шагом перфорации в 2,5 мм и диаметром приблизительно 2 мм. Размеры заготовки и параметры штампа приведены на рис. 7.1, штамповку выполняли поэтапно до размера толщины заусенца 2 h < 2 мм на универсальной испытательной машине УИМ-50. Для имитации условий трения поверхность штампа "припудривали" стеклянным порошком, создающим мак­симальный коэффициент трения ( f ≈ 0,5), поскольку одновременно проверяли расчетный метод определения перемещений металла с учетом трения. Одна из сеток, размещенная в горизонтальной плоскости заусенца, после деформирования приняла вид, представленный на рис. 7.1, где условно построена также эпюра деформации 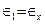в срединном сечении, на которой максимумы деформаций характеризуют зону формирования заусенца.

Измерение деформаций и перемещений с помощью сетки с квадратными ячейками, когда в общем случае базовый элемент превращается в параллеле­пипед или четырехугольник, выполняют оптическими средствами с последую­щим вычислением абсолютных приращений граней параллелепипеда и соответствующих углов на основании достаточно громоздких формул, полученных из геометрических соотношений. Вычисления и сглаживание функций осущест­вляют несколькими способами.

Для исследования задач обработки металлов давлением представляет ин­терес определение скоростей перемещений, скоростей деформаций, линий тока.

Скорости перемещений v_x, v_у, v_z и деформаций 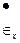, , 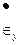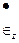получают численным дифференцированием, реже — графическим. Измерения деформаций по ячейкам весьма трудоемки, а для достижения надежных результатов при дифференци­ровании точность измерений приращений и координат должна быть достаточно высока.

Расчет напряжений выполняют на основе гипотез теории пластичности. В зависимости от поставленной задачи и типа материала вычисления проводят по теориям малых упругопластических деформаций, пластического течения, сопротивления материалов пластическому деформированию.

Наиболее полно методика измерений и последующей обработки результатов при исследовании задач обработки металлов давлением методом сеток изложена в книге Деля Г.Д., причем для определения интенсивности напряжений предложен экспериментальный метод, связывающий твердость (по Бринеллю или по Виккерсу) со значениями интенсивности напряжений. Для этого строят график зависимости интенсивности напряжений от НВ или HV при различных уровнях деформации растяжения или сжатия.

При изучении НДС деталей машин успешно используют резиновые модели. Опыт лабораторий Германии показал, что на резиновых моделях методами делительных сеток и муаровых полос проводят не только демонстрационные опыты, но и крупные технические исследования, например, ответственных деталей дизеля и турбин. Эксперименты выполняют на сложных отформованных и завулканизированных моделях из светлой резины, на поверхность которых наносят нечастые квадратные сетки с шагом 2 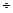10 мм X мм. В области контактных сопряжений и на края модели наносят более частые риски, определяющие линейные деформации по касательной к краю.

Резины, как конструкционный материал для моделей, должны обладать рядом обязательных механических и реологических свойств. Так, упругие, вязкоупругие свойства, ползучесть и последействие определяют предельную упругую область деформирования при исследовании НДС деталей машин и конструкций. Обычные резины и полиуретановые каучуки имеют достаточно большую упругую область деформирования, приблизительно 60—70 %, но для исследований методом сеток деформации ограничивают до 10—15 %. Это связано с тем, что моделирование напряжений на резиновых моделях сопряжено с погрешностями, связанными с геометрической изменяемостью сечений моделей и изменением коэффициента Пуассона в зависимости от степени деформирования и двухосности напряженного состояния.

Кроме того, сама величина μ ≈ 0,5 при малых деформациях отличается от значений

μ =0,25 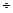0,3 для большинства мо­делируемых материалов натуры.

При одноосном растяжении и условии неизменяемости объема имеем хорошо обоснованную экспериментальную зависимость:

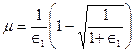, (7.4)

где: μ— переменный коэффициент поперечной деформации;

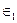— главная дефор­мация в координатах Лагранжа; .

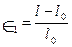Изменение μ происходит от 0,5 при малых деформациях до 0,3 при 100%-ных деформациях.

Таблица 7.1

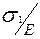
	Значение коэффициента μпри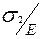
0,0	0,2	0,4	0,6	0,8	1,0
	0,5	0,44	0,39	0,36	0,32	0,29
10%	0,47	0,46	0,43	0,38	0,34	0,31
20%	0,44	0,46	0,44	0,40	0,36	0,33

Примечание. При плоской деформации μ ≈ 0,50.

Для значений 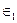= 15 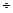20 % коэффициент μ = 0,44 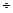0,42 для полиуретанового каучука СКУ-6. Экспериментально обосновано, что при боль­ших деформациях резин может быть применен обобщенный закон Гука при μ≠const. При деформировании резин до 10 - 15% отсутствует заметная нелинейность, вязкоупругость и гистерезис; в этом случае значения коэффициента μв зависимости от двухосности НДС можно ориентировочно принимать по таблице для плоского напряженного состояния.

Напряжения на поверхности резиновых моделей вычисляют на основании измерений линейных перемещений в квадратной ячейке с исходной стороной l₀:

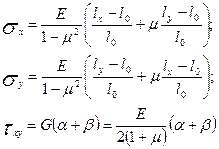(7.5)

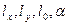где и 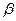- линейные и угловые перемещения в ячейках до и после деформации (рис. 7.2).

Учитывая, что ,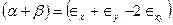

где 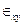— удлинение в направлении биссектрисы угла между положительной осью хи отрицательной ветвью оси у, так в 45°- ной розетке, изображенной на рис. 7.2.

		l 0
l 0

Рис. 7.2. Деформация квадратной сетки и ориентация осей в