Плоское напряженное состояние с осевой симметрией
Вследствие осевой симметрии окружные напряжения 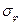 и радиальные напряжения
и радиальные напряжения 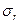 являются главными. Их можно определить из системы
являются главными. Их можно определить из системы
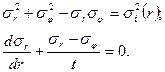 (6.7)
(6.7)
Систему (6.7) решали численным методом. Для этого радиус исследуемого тела разбивали точками 0, 1,2, ... на ряд достаточно малых отрезков длиной Δ. По твердости определяли интенсивность напряжений в этих точках.
Пусть в точке 0 напряжения известны. В частности, если в этой точке 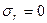 , то
, то
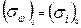 ,
, 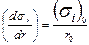 ;
;
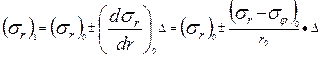 ; (6.8)
; (6.8)
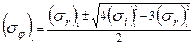 . (6.9)
. (6.9)
В формуле (6.8) знак «плюс» соответствует случаю, когда 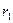 >
> 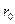 . В формуле (6.9) знак выбирали таким образом, чтобы не возник разрыв напряжений
. В формуле (6.9) знак выбирали таким образом, чтобы не возник разрыв напряжений 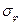 . Если это условие выполняется при любом знаке, то для выбора решения необходимы дополнительные условия.
. Если это условие выполняется при любом знаке, то для выбора решения необходимы дополнительные условия.
Для определения напряжений в остальных точках записываем дифференциальное уравнение равновесия в конечных разностях.
Так, для определения (Ϭr)2 записываем уравнение для точки 1
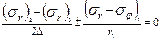 (6.10)
(6.10)
из которого находим
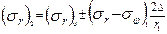 . (6.11)
. (6.11)
Знак «плюс» по-прежнему соответствует случаю, когда
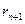 >
> 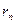 .Напряжение
.Напряжение 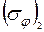 определяли по формуле, аналогичной (6.9).
определяли по формуле, аналогичной (6.9).
Таким же образом можно определить напряжения в точках 3, 4, 5, ...и т.д. во всей исследуемой области.
Дата добавления: 2014-12-30; просмотров: 1109;
