Уравнение состояния.

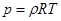– уравнение в интегральной форме (5.25)

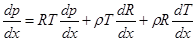– уравнение в дифференциальной форме (5.26)

разделив (5.26) на (5.25) получим:

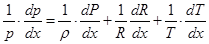(5.27)

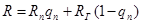(5.28)

где индексы п и г означают пар и газ.

Массовая доля компонента в фазе:

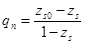(5.29)

берем производную по dx:

;

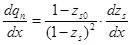Тогда,

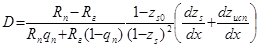(5.30)

В результате получаем:

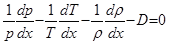(5.31)

Уравнение неразрывности:

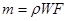– уравнение в интегральной форме (5.32)

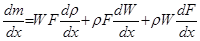– уравнение в дифференциальной форме (5.33)

разделим (5.32) на (5.33):

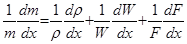(5.34)

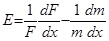(5.35)

берем производную dx:

()

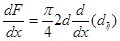
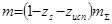
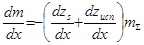
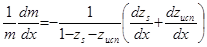
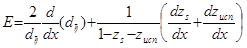(5.36)

В результате преобразований получаем.

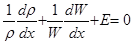(5.37)

Уравнение движения (в дифференциальной форме):

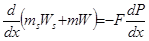(5.38)

Из уравнения неразрывности

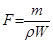
Тогда,

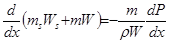разделим на m_Σ

;

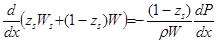
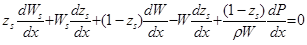разделим на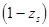

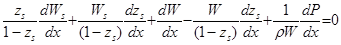
В результате преобразований получаем:

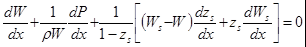(5.39)

Вывод уравнения энергии:

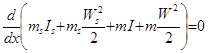(в дифференциальной форме) (5.40)

разделим на m_Σ

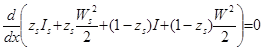
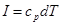
Продифференцируем и разделим на :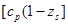

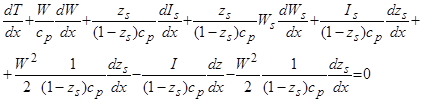
В результате преобразований получается:

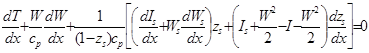(5.41)