Модели теории массового обслуживания

Теория массового обслуживания представляет собой область при­кладной математики, использующую методы теории случайных про­цессов и теории вероятностей для исследования различной природы сложных систем. Теория массового обслуживания непосредственно не связана с оптимизацией. Назначение ее состоит в том, чтобы на осно­ве результатов наблюдений за «входом» в систему предсказать ее воз­можности и организовать наилучшее обслуживание для конкретной ситуации и понять, как последнее отразится на стоимости системы в целом.

Модели теории массового обслуживания описывают процессы массового спроса на обслуживание с учетом случайного характера поступления требований и продолжитель­ности обслуживания.

Назначение моделей теории массового обслуживания состоит в том, чтобы на основе информации о входящем случайном потоке требова­ний предсказать возможности системы обслуживания, организовать наилучшее выполнение требований для конкретной ситуации и оце­нить, как это отразится на ее стоимости.

Система массового обслуживания (СМО) возникает тогда, когда происходит массовое появление заявок (требований) на обслуживание и их последующее удовлетворение.

Особенностью СМО является случайный характер исследуе­мых явлений. Типичный пример СМО - телефонная сеть (снятием трубки с рычага телефонного аппарата абонент дает заявку на обслуживание разговора по одной из линий телефонной сети).

Основными элементами СМО являются:

- входящий поток заявок (требований) на обслуживание;

- очередь заявок на обслуживание;

- приборы (каналы) обслуживания;

- выходящий поток обслуженных заявок (рисунок 8.5).

Такой элемент СМО как очередь может отсутствовать в не­которых системах, но в тоже время СМО может иметь и другие элементы, например, выходящий поток не обслуженных заявок.

Для систем, относящихся к системам массового обслуживания, существует определенный класс задач, решение которых позволяет от­ветить, например, на следующие вопросы:

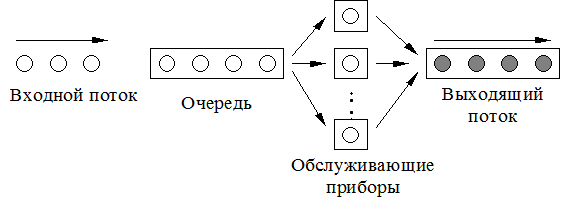
Рисунок 8.5 - Обобщенная схема СМО

С какой ин­тенсивностью должно проходить обслуживание или должен выполнять­ся процесс при заданной интенсивности и других параметрах входящего потока требований, чтобы минимизировать очередь или задержку в подготовке документа или другого вида информации?

Каковы вероят­ность появления задержки или очереди и ее величина? Сколько време­ни требование находится в очереди и каким образом минимизировать его задержку?

Какова вероятность потери требования (клиента)?

Ка­кова должна быть оптимальная загрузка обслуживающих каналов? При каких параметрах системы достигаются минимальные потери прибы­ли?

К этому перечню можно добавить еще целый ряд задач.

Как системы массового обслуживания могут быть представ­лены следующие работы и процессы: посадка самолетов в аэро­порту, обслуживание автомобилей на автозаправочных станциях, разгрузка судов на причалах, обслуживание покупателей в ма­газинах, прием больных в поликлинике, обслуживание клиентов в ремонтной мастерской и др.

Часто входной поток заявок представляется в виде про­стейшего потока, обладающего свойством стационарности, от­сутствия последствия и ординарности.

Поток является стационарным, если вероятный режим не зависит от времени. Ординарность потока наступает, если ве­роятность появления двух и более заявок за промежуток вре­мени τявляется бесконечно малой величиной по сравнению с τ. Поток обладает свойством отсутствия последствия, если поступление заявок не зависит от предистории процесса.

Для простейшего потока поступление заявок в СМО описы­вается законом распределения Пуассона

Р_к(τ) ,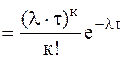

где Р_к(τ) -вероятность поступления к заявок за время τ;

λ - интенсивность входного потока.

Важное для исследования свойство, которым обладает пуассоновский поток, заключается в том, что процедура разделения и объединения дает снова пуассоновские потоки. Тогда, если входной по­ток формируется из N независимых источников, каждый из которых порождает пуассоновский поток интенсивностью λ_i (i = 1, 2, ..., N), то его интенсивность будет определяться по формуле

λ = λ _l + λ ₂ +...+ λ _N.

В случае разделения пуассоновского потока на N независимых по­токов получим, что интенсивность потока λ_i будет равна r_i λ ,где r_i - доля i-го потока во входном потоке требований.

Очередью является множество заявок (требований), ожи­дающих обслуживание.

В зависимости от допустимости и характера формирования очереди системы массового обслуживания подразделяются:

1. СМО с отказами - формирование очереди не разрешено, поэтому заявка, пришедшая в момент, когда все каналы заняты, получает отказ и теряется. Пример: АТС (выполнение заказов к определенному сроку), система ПВО объекта (цель в зоне об­стрела пребывает мало времени).

2. СМО с неограниченным ожиданием - поступившая заяв­ка, застав все обслуживающие приборы занятыми, становится в очередь и дожидается обслуживания. Число мест для ожидания (длина очереди) не ограничено. Не ограничивается и время ожидания. Пример: предприятия бытового обслуживания, такие как мастерские по ремонту часов, обуви.

3. СМО смешанного типа. В этих системах имеется очередь,
на которую накладываются ограничения. Например: на макси­мальную длину очереди (I тип – с ограниченной ДО) или на время ожидания заявки в очереди (П тип – с ограниченным ВО). Примерами СМО I-го типа являются мастер­ские по ремонту радиоаппаратуры с ограниченными площадями для ее хранения. Торговые точки по продаже фруктов, овощей, которые могут храниться ограниченное время, являются смешан­ными СМО II -го типа.

Порядок поступления заявок на обслужива­ние называется дисциплиной обслуживания.

В СМО с очередью могут быть следующие варианты дисцип­лины обслуживания:

а) в порядке поступления заявок (первым пришел – первым обслужился) - магазины, предприятия бытового обслуживания;

б) в порядке обратном поступлению, т. е. последняя заявка обслуживается первой (последним пришел - первым обслужился) - выемка заготовок из бункера;

в) в соответствии с приоритетом (участники ВОВ в поликлинике);

г) в случайном порядке (в системе ПВО объекта при отра­жении воздушного налета противника).

Основным параметром процесса обслужи­вания считается время обслуживания заявки каналом (обслуживающим прибором j ) – t_j (j=1,2,…,m).

Величина t_j в каждом конкретном случае определяется рядом факторов: интенсивностью поступления заявок, квалификацией ис­полнителя, технологией работ, окружающей средой и т.д. Законы рас­пределения случайной величины t_j могут быть самыми различными, но наибольшее распространение в практических приложениях полу­чил экспоненциальный закон распределения. Функция распределения случайной величины t_j имеет вид:

F(t) = l – e ^{- μt} ,

где m - положительный параметр, определяющий интенсивность обслужи­вания требований;

,

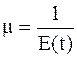где Е (t) - математическое ожидание случайной величины обслуживания тре­бования t_j .

Важнейшее свойство экспоненциального распределения заключа­ется в следующем. При наличии нескольких однотипных каналов об­служивания и равной вероятности их выбора при поступлении заявки распределение времени обслуживания всеми m каналами будет пока­зательной функцией вида:

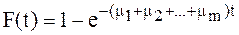
Если СМО состоит из неоднородных каналов, то 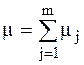, если
же все каналы однородные, то .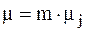

По количеству обслуживающих приборов (каналов) СМО де­лятся на:

- одноканальные;

- многоканальные.

Структура СМО и характерис­тика ее элементов приведены на рисунке 8.6.

Исследование СМО заключается в нахождении показателей, харак­теризующих качество и условия работы обслуживающей системы и показателей, отражающих экономические последствия принятых ре­шений.

Важнейшим понятием в анализе СМО является понятие сос­тояния системы. Состояние есть некоторое описание системы, на основании которого можно предсказать ее будущее поведение.

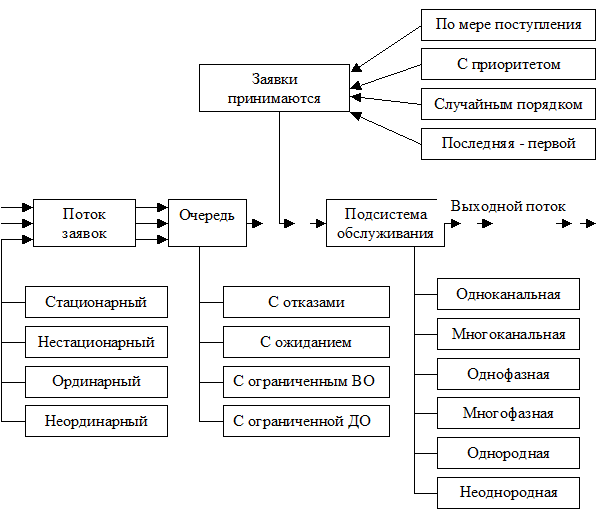
Рисунок 8.6 – Структура и характеристика элементов СМО

При анализе СМО определяют усредненные показатели об­служивания. В зависимости от решаемой задачи ими могут быть:

средняя длина очереди,

среднее время ожидания в очереди,

средний процент обслуживаемых (или получивших отказ) заявок, среднее число занятых (или простаивающих) каналов,

среднее время пребывания в СМО и др.

В качестве критерия оптимизации применяют:

- максимум прибыли от эксплуатации СМО;

- минимум суммарных потерь, связанных с простоем кана­лов, простоем заявок в очереди и уходом необслуженных за­явок;

- обеспечение заданной пропускной способности.

Варьируемыми параметрами обычно являются: количество каналов, их производительность, длина и дисциплина очереди, приоритетность обслуживания.

Вопросы для самопроверки

1. Понятие о математических моделях и моделировании.

2. Что представляет собой экономико-статистическая модель и производственная функция?

3. Применение графических и графоаналитических моделей в управлении.

4. Использование корреляционного анализа для выявления связи между параметрами

5. Виды и методы построения регрессионных моделей.

6. Статистическое исследование причинно-следственных связей.

7. Классификация математических моделей по четырем аспектам детализации (по В.А. Кардашу).

8. Классификация моделей по применяемому математическому аппарату. Понятие о балансовых моделях.

9. Этапы моделирования. Проверка модели на адекватность.

10. Понятие о системах массового обслуживания (СМО). Составные части СМО.

11. СМО с отказами и с очередью. Разновидности очередей.

12. Одноканальные и многоканальные СМО. Дисциплины обслуживания

13. Моделирование СМО. Показатели, получаемые при экспериментах на модели СМО.

14. Критерии оптимизации систем массового обслуживания.