Виды математических моделей
В зависимости от того, какими средствами, при каких условиях и по отношению к каким объектам познания реализуется способность моделей отображать действительность, возникает их большое разнообразие, а вместе с ним — классификации. Путем обобщения существующих классификаций выделим базовые модели по применяемому математическому аппарату, на основе которых получают развитие специальные модели (рисунок 8.1).
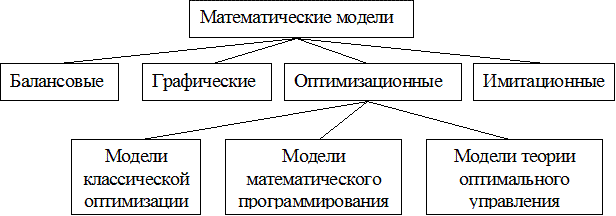
Рисунок 8.1 - Формальная классификация моделей
Математические модели отображают изучаемые объекты (процессы, системы) в виде явных функциональных соотношений: алгебраических равенств и неравенств, интегральных и дифференциальных, конечно-разностных и других математических выражений (закон распределения случайной величины, регрессионные модели и т.д.), а также отношений математической логики.
В зависимости от двух фундаментальных признаков построения математической модели — вида описания причинно-следственных связей и изменений их во времени — различают детерминистические и стохастические, статические и динамические модели (рисунок 8.2).
Цель схемы, представленной на рисунке, — отобразить следующие особенности:
1) математические модели могут быть и детерминистическими, и стохастическими;
2) детерминистические и стохастические модели могут быть и статическими, и динамическими.
Математическая модель называется детерминистической (детерминированной), если все ее параметры и переменные являются однозначно определяемыми величинами, а также выполняется условие полной определенности ин  формации. В противном случае, в условиях неопределенности информации, когда параметры и переменные модели — случайные величины, модель называется стохастической (вероятностной).
формации. В противном случае, в условиях неопределенности информации, когда параметры и переменные модели — случайные величины, модель называется стохастической (вероятностной).
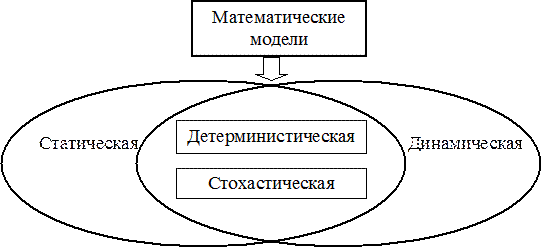
Рисунок 8.2 – Классы математических моделей
Модель называется динамической, если как минимум одна переменная изменяется по периодам времени, и статической, если принимается гипотеза, что переменные не изменяются по периодам времени.
В простейшем случае балансовые модели выступают в виде уравнения баланса, где в левой части располагается сумма каких-либо поступлений, а в правой - расходная часть также в виде суммы. Например, в таком виде представляется годовой бюджет организации.
На основе статистических данных могут строиться не только балансовые, но и корреляционно-регрессионные модели.
Если функция Y зависит не только от переменных х1, , х2, … хn , но и от других факторов, связь между Y и х1, , х2, … хn является неточной или корреляционной в отличие от точной или функциональной связи. Корреляционными, например, в большинстве случаев являются связи, наблюдающиеся между выходными параметрами ОПС и факторами ее внутренней и внешней среды (см. тему 5).
Корреляционно-регрессионные модели получают при исследовании влияния целого комплекса факторов на величину того или иного признака путем применения статистического аппарата. При этом ставится задача не только установить корреляционную связь, но и выразить эту связь аналитически, то есть подобрать уравнения, описывающие данную корреляционную зависимость (уравнение регрессии).
Для нахождения численного значения параметров уравнения регрессии пользуются методом наименьших квадратов. Суть этого метода состоит в том, чтобы выбрать такую линию, при которой сумма квадратов отклонений от нее ординат Y отдельных точек была бы наименьшей.
Корреляционно-регрессионные модели часто используются при исследовании явлений, когда возникает необходимость установить зависимость между соответствующими характеристиками в двух и более рядах. При этом преимущественно используется парная и множественная линейная регрессия вида
y = ax + b ,
y = a1x1 + a2x2 + … + anxn + b .
В результате применения метода наименьших квадратов устанавливаются значения параметров a или a1, a2, …, an и b, а затем выполняются оценки точности аппроксимации и значимости полученного уравнения регрессии.
В особую группу выделяют графоаналитические модели. Они используют различные графические изображения и поэтому обладают хорошей наглядностью.
Теория графов - одна из теорий дискретной математики, изучает графы, под которыми понимается совокупность точек и линий их соединяющих. Граф - это самостоятельный математический объект (впервые ввел Кёниг Д.). На основе теории графов наиболее часто строят древовидные и сетевые модели.
Древовидная модель (дерево) - это неориентированный связный граф, не содержащий петель и циклов. Примером такой модели является дерево целей.
Сетевые модели нашли широкое применение в управлении производством работ. Сетевые модели (графики) отражают последовательность выполнения работ и продолжительность каждой работы (рисунок 8.3).

Рисунок 8.3 - Сетевая модель производства работ
Каждая линия сетевого графика - это некоторая работа. Цифра рядом с ней означает продолжительность ее выполнения.
Сетевые модели позволяют найти так называемый критический путь и оптимизировать график производства работ по времени при ограничениях на другие ресурсы.
Сетевые модели могут быть детерминированными и стохастическими. В последнем случае продолжительности выполнения работ задаются законами распределения случайных величин.
Оптимизационные модели служат для определения оптимальной траектории достижения системой поставленной цели при наложении некоторых ограничений на управление ее поведениям и движением. В этом случае оптимизационные модели описывают различного рода задачи нахождения экстремума некоторой целевой функции (критерия оптимизации).
Для выявления оптимального способа достижения цели управления в условиях ограниченных ресурсов – технических, материальных, трудовых и финансовых – применяют методы исследования операций. К ним относятся методы математического программирования (линейное и нелинейное, целочисленное, динамическое и стохастическое программирование), аналитические и вероятностно-статистические методы, сетевые методы, методы теории массового обслуживания, теории игр (теории конфликтных ситуаций) и др.
Оптимизационные модели применяются для объемного и календарного планирования, управления запасами, распределения ресурсов и работ, замены, параметризации и стандартизации оборудования, распределения потоков товарных поставок на транспортной сети и других задач управления.
Одним из основных достижений теории исследования операций считается типизация моделей управления и методов решения задач. Например, для решения транспортной задачи, в зависимости от ее размерности, разработаны типовые методы — метод Фогеля, метод потенциалов, симплекс-метод. Также при решении задачи управления запасами, в зависимости от ее постановки, могут использоваться аналитические и вероятностно-статистические методы, методы динамического и стохастического программирования.
В управлении особое значение придается сетевым методам планирования. Эти методы позволили найти новый и весьма удобный язык для описания, моделирования и анализа сложных многоэтапных работ и проектов. В исследовании операций значительное место отводится совершенствованию управления сложными системами с применением методов теории массового обслуживания (см. раздел8.3) и аппарата марковских процессов.
Модели марковских случайных процессов — система дифференциальных уравнений, описывающих функционирование системы или ее процессов в виде множества упорядоченных состояний на некоторой траектории поведения системы. Этот класс моделей широко используется при математическом моделировании функционирования сложных систем.
Модели теории игр служат для выбора оптимальной стратегии в условиях ограниченной случайной информации или полной неопределенности.
Игра — математическая модель реальной конфликтной ситуации, разрешение которой ведется по определенным правилам, алгоритмам, описывающим некоторую стратегию поведения лица, принимающего решение в условиях неопределенности.
Различают «игры с природой» и «игры с противником». Исходя из ситуации определяются методы и критерии оценки принятия решений. Так, при «играх с природой» применяют критерии: Лапласа, максиминный (критерий Вальда) и минимаксный, Гурвица и Сэвиджа и ряд других алгоритмических правил. При «играх с противником» для принятия решений используются платежные матрицы, максиминный и минимаксный критерии, а также специальные математические преобразования в связи с тем, что лицу, принимающему решение, противостоит недоброжелательный противник.
Рассмотренные типы математических моделей не охватывают всего их возможного многообразия, а лишь характеризуют отдельные виды в зависимости от принятого аспекта классификации. В.А.Кардашем была предпринята попытка создания системы классификации моделей по четырем аспектам детализации (рисунок 8.4).
| Временной аспект | |||||||
| статические | динамические | ||||||
| Социальный, организационный, технологический аспекты | Однокритериальные модели | Детерминированные | Стохастический аспект | ||||
| Стохастические | |||||||
| Модели, учитывающие взаимодействие интересов | Детерминированные | ||||||
| Стохастические | |||||||
| А | В | А | В | ||||
| Пространственный аспект |
А - модели без пространственной дифференциации параметров;
В - модели с пространственной дифференциацией параметров
Рисунок 8.4 - Классификация моделей по четырем аспектам детализации
С развитием вычислительных средств одним из распространенных методов принятия решений выступает деловая игра, представляющая собой численный эксперимент с активным участием человека. Существуют сотни деловых игр. Они применяются для изучения целого ряда проблем управления, экономики, теории организации, психологии, финансов и торговли.
Дата добавления: 2014-12-27; просмотров: 25029;
