С. Другие применения алгебры логики

1. Символическая логика, в том числе алгебра логики, широко применяется в кибернетике. Об отце символической логики Лейбнице Норберт Винер, сформулировавший основные идеи кибернетики, пишет: “Если бы мне пришлось выбирать в анналах истории наук святого — покровителя кибернетики, то я выбрал бы Лейбница. Философия Лейбница концентрируется вокруг двух идей, тесно связанных между собой: идеи универсальной символики и идеи логического исчисления.

Из этих двух идей возникли современный математический анализ и современная математическая логика. И как в арифметическом исчислении была заложена возможность развития ее механизации от абака и арифмометра до современных сверхбыстрых машин, так и в исчислении умозаключений Лейбница содержится в зародыше думающая машина. Сам Лейбниц, подобно своему предшественнику Паскалю, интересовался созданием вычислительных машин в металле. Поэтому совсем неудивительно, что тот же самый умственный толчок, который привел к развитию математической логики, одновременно привел к гипотетической или действительной механизации процессов мышления”[68].

2. Алгебра логики применяется при проектировании переключательных схем, являющихся элементами автоматизированных систем управления и вычислительных машин. При этом символ “•” интерпретируется как последовательное соединение переключателей, а символ “Ú” — как параллельное. Например, формулам p • (q Ú r) и р • q Ú р • r соответствуют следующие схемы:

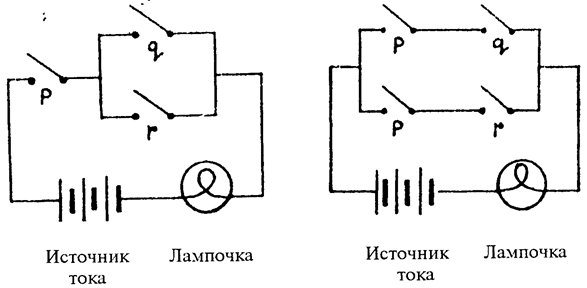
р = 1 — переключатель замкнут, р = 0 — разомкнут. Если в схеме имеются два (или более) переключателя р, то они могут быть замкнуты (или разомкнуты) только одновременно (именно поэтому они обозначаются одной и той же буквой).

По электрической цепи, изображенной на левой схеме, ток идет тогда и только тогда, когда он идет по цепи, изображенной на правой схеме, так как формулы р • (q Ú r ) и р • q Ú р • r — тождественные.

Символ “-” интерпретируется как противоположное состояние

_ _

переключателя, т.е. если р = 1, то p = 0, а если переключатель р замкнут, то p

_

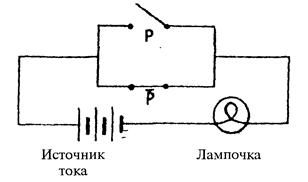
разомкнут. Так, формуле р Ú p соответствует схема:

_

По этой цепи ток идет всегда, так как р Ú р = 1, т.е. если переключатель р

_

разомкнут, то переключатель р замкнут, и наоборот. Лампочка горит постоянно. Можно упростить схему, убрав оба переключателя.

Алгебра логики располагает средствами, позволяющими найти наиболее простую схему (например, содержащую наименьшее число переключателей) по сравнению с данной, но выполняющую те же функции, что и исходная.

3. “Прекрасно приспособленная для описания комбинаторных явлений, эта теория получает многочисленные применения к исследованию операций, где се нередко связывают с теорией структур.”[69]

Алгебра логики применяется также в сетевом планировании и линейном программировании.

4. Алгебра логики применяется при установлении правильности или неправильности рассуждении. Пример рассуждения: “Если Иванов является участником этого преступления, то он знал потерпевшего. Иванов не знал потерпевшего, но знал его жену. Потерпевший знал Иванова. Следовательно, Иванов не является участником этого преступления.” Переведем рассуждение на язык алгебры логики. Обозначим символами простые суждения, входящие в рассуждение: “Иванов является участником этого преступления” (р), “Иванов знал потерпевшего” (q), “Иванов знал жену потерпевшего” (r), “потерпевший знал Иванова” (s). Затем переведем на язык алгебры логики посылки и

_

заключение рассуждения. При этом вместо “если р, то q” напишем p Ú q. Союз “но” по смыслу соответствует союзу “и”.

Переводом посылок и заключения являются формулы:

_ _ _

р Ú q, q • r, s и p соответственно.

Формулы, переводящие посылки, последовательно соединим друг с другом символом “•”: ((p Ú q) • (q • r)) • s.

Поставив над полученной формулой знак отрицания, присоединим к ней символом “Ú” формулу, соответствующую заключению:

________________

_ _ _

((p Ú q) • (q • r)) • s Ú p

Полученная формула является переводом на язык символов исходного рассуждения. Если исходное рассуждение является правильным, то полученная формула равно 1.

______________

_ _ _

1) ((p Ú q) • (q • r)) • s Ú p — исходная формула

___________

_ _ _

2) (pÚ q) • (q • r)Ú s Ú p — из 1) по Т9,

____ ____

_ _ _ _

3) pÚ q Ú q • r Ú s Ú p — из 2) по Т9,

= _ = _ _

4) p • q Ú q Ú r Ú s Ú p — из 3) по Т9,

= = _ _ _

5) p Ú q Ú r Ú s Ú p — из 4) по Т11,

_ = _ _

6) p Ú p Ú q Ú r Ú s — из 5) по Т12 и Т1,

= _ _

7) 1 Ú q Ú r Ú s — из 6) по Т7,

8) 1 — из 7) по Т6.

Анализируемое рассуждение является правильным.