ПЕРЕНОС ТЕПЛОТЫ ТЕПЛОПРОВОДНОСТЬЮ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ

Однородная плоская стенка. Про­стейшей и очень распространенной за­дачей, решаемой теорией теплообмена, является определение плотности тепло­вого потока, передаваемого через плоскую стенку толщиной δ, на повер­хностях которой поддерживаются темпе­ратуры t_c1 и t_c2 (рис. 8.2). Температура изменяется только по толщине пласти­ны — по одной координате х. Такие за­дачи называются одномерными, решения их наиболее просты, и в данном курсе мы ограничимся рассмотрением только од­номерных задач. Учитывая, что для од­номерного случая grad t = dt/dx [81] и используя основной закон теплопро­водности [79], получаем дифференци­альное уравнение стационарной тепло­проводности для плоской стенки: 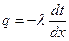[82]

В стационарных условиях, когда энергия не расходуется на нагрев, плот­ность теплового потока qнеизменна по толщине стенки. В большинстве практи­ческих задач приближенно пред­полагается, что коэффициент тепло­проводности λне зависит от температуры и одинаков по всей толщине стенки. Зна­чение λ находят в справочниках [15] при температуре t =0,5 (t_с1+t_с2), [83] средней между температурами поверхно­стей стенки. (Погрешность расчетов при этом обычно меньше погрешности исход­ных данных и табличных величин, а при линейной зависимости коэффициента теплопроводности от температуры λ= a + bt точная расчетная формула для q не отличается от приближенной). При λ = const dt/dx = - q/λ = const, [84]

т. е. зависимость температуры tот ко­ординаты х линейна (рис. 19).

Разделив переменные в уравнении (84) и проинтегрировав по t от t_c1 до t_c2 и по х от 0 до δ: 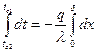[85] получим зависимость для расчета плот­ности теплового потока 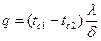[86]

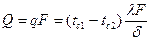или [87]

Полученная простейшая формула имеет очень широкое распространение в тепло­вых расчетах. По этой формуле не только рассчитывают плотности теплового пото­ка через плоские стенки, но и делают оценки для случаев более сложных, уп­рощенно заменяя в расчетах стенки сложной конфигурации на плоскую. Иногда уже на основании оценки тот или иной вариант отвергается без дальней­ших затрат времени на его детальную проработку.

По формуле [87] можно рассчитать коэффициент теплопроводности материа­ла, если экспериментально замерить теп­ловой поток и разность температур на поверхностях пластины (стенки) извест­ных размеров.

Отношение 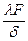называется тепло­вой проводимостью стенки, а обратная величина 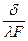тепло­вым или термическим сопротив­лением стенки и обозначается R_λ).. Пользуясь понятием термического сопро­тивления, формулу для расчета теплово­го потока можно представить в виде 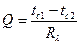[88]

аналогичном закону Ома в электротехни­ке (сила электрического тока равна раз­ности потенциалов, деленной на электри­ческое сопротивление проводника, по ко­торому течет ток).

Очень часто термическим сопротив­лением называют величину δ/λ, кото­рая равна термическому сопротивлению плоской стенки площадью 1 м².

Многослойная стенка. Формулой [88] можно пользоваться и для расчета теплового потока через стенку, состоя­щую из нескольких плотно прилегающих друг к другу слоев разнородных материа­лов (рис. 20), например кирпичную стен­ку здания, покрытую слоем штукатурки, краски и т. д. Термическое сопротивление такой стенки равно сумме термических сопротивлений отдельных слоев:

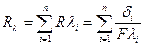[89]

В формулу [88] нужно подставить разность температур в тех точках (по­верхностях), между которыми «включе­ны» все суммируемые термические сопротивления

т.е. в данном случае t_c1 и t_{c (n+1)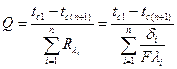}: [90]

Формулу [90] легко получить, за­писав разность температур по формуле [87] для каждого из п слоев многослой­ной стенки и сложив все п выражений с учетом того, что во всех слоях Q имеет одно и то же значение. При сложении все промежуточные температуры сократятся.

Распределение температур в преде­лах каждого слоя — линейное, однако в различных слоях крутизна температур­ной зависимости различна, поскольку со­гласно формуле (dt/dx)_I = -q/λ_i.

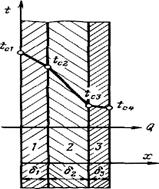
Рис. 2.5 Распределение температуры по тол­щине многослойной плоской стенки

Плотность теплового потока, проходяще­го через все слои, в стационарном режи­ме одинакова, а коэффициент теплопро­водности слоев различен, следовательно, более резко температура меняется в сло­ях с меньшей теплопроводностью. Так, в примере на рис. 2.5 наименьшей тепло­проводностью обладает материал второ­го слоя, а наибольшей — третьего.

Рассчитав тепловой поток через мно­гослойную стенку, можно определить па­дение температуры в каждом слое по соотношению [88] и найти температу­ры на границах всех слоев. Это очень важно при использовании в качестве теплоизоляторов, материалов с ограничен­ной допустимой температурой.

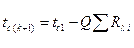[91]