ПОНЯТИЕ О МЕТОДЕ АНАЛИЗА РАЗМЕРНОСТЕЙ И ТЕОРИИ ПОДОБИЯ
Основная трудность возникающая при экспериментальном исследовании конвективного теплообмена, заключается в том, что коэффициент теплоотдачи зависит от многих параметров. Например, средний по поверхности коэффициент теплоотдачи от продольно омываемой пластины (см. рис. 9.2) зависит от длины пластины l, скорости набегающего потока wж и теплофизических параметров жидкости:
α = f1( l wж , λ, c, ρ, ν ) [111]
Вт /м2. К м м/с Вт/м.К Дж/кг.К кг/м3 м2/с
Если проводить эксперименты, изменяя т раз каждый из шести параметров, влияющих на теплообмен, то суммарное число экспериментов будет N = m6, т. е. порядка 106.
Теория показывает, что число параметров зависит от выбора единиц измерения. Наименьшее число параметров получится, если единицы измерения будут связаны с самой решаемой задачей. Так, в качестве единицы длины можно принять не метр, а длину пластины l. Для перевода всех параметров в «новую» систему единиц измерения поделим их на l в той же степени, в которой длина входит в их размерность:
αl2 = f1( l/l wж /l, λ/l, c, ρ/l3, ν/l2 [112]
Вт /К - 1/с Вт/ К Вт.с/кг.К кг 1/с
Число параметров в правой части уравнения уменьшилось, так как l / l=1 т. е. мы избавились от того параметра, который приняли за единицу измерения. Если теперь ввести еще три «новых» единицы измерения: для времени l2/v, для массы рl3 и, наконец, для отношения тепловой мощности к перепаду температур λl (в рассматриваемой системе величин единицы Вт и К раздельно не встречаются, а входят лишь в комбинации Вт/К), то в правой части рассматриваемой зависимости останется всего два безразмерных параметра:
αl/λ = f3 (wжl /ν, cρν/λ) [113]
Такие же безразмерные параметры получаются и при анализе теплоотдачи от поверхности трубы, но определяющим размером в них будет не длина l, а диаметр d, соответственно внутренней — при течении жидкости внутри трубы и наружный — при наружном обтекании одной трубы или пучка труб.
Согласно основной теореме метода анализа размерностей (π-теореме) зависимость между N размерными величинами, определяющими данный процесс, может быть представлена в виде зависимости между составленными из них N — К безразмерными величинами, где К — число первичных переменных с независимыми размерностями, которые не могут быть получены друг из друга. В уравнении [111] общее число переменных (включая и а) равно 7, из них четыре первичных (их мы принимали за единицы измерения) соответственно безразмерных чисел в уравнении [113] N – K = 7-4 = 3.
Каждый из безразмерных параметров имеет определенный физический смысл. Их принято обозначать первыми буквами фамилий ученых, внесших существенный вклад в изучение процессов теплопереноса и гидродинамики, и называть в честь этих ученых.
Число Нуссельта (1887—1957 гг.): Nu = αl/λ [114]
представляет собой безразмерный коэффициент теплоотдачи.
Число Рейнольдса (1842-1912) Re = wжl /ν выражает отношение сил инерции (скоростного напора) Fи = ρw 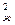 /2
/2  к силам вязкого трения Fμ~μwж/l.
к силам вязкого трения Fμ~μwж/l.
Безразмерные комплексы обычно не являются точным отношением каких-то сил, а лишь качественно характеризуют их соотношение.
При малых числах Re преобладают силы вязкости и режим течения жидкости ламинарной (отдельные струи потока не перемешиваются, двигаясь параллельно друг другу, и всякие случайные завихрения быстро затухают под действием сил вязкости). При турбулентном течении в потоке преобладают силы инерции, поэтому завихрения интенсивно развиваются.
При течении жидкостей в трубах (см. рис. 9.4) ламинарный режим на стабилизированном участке наблюдается до ReKp = wd/v = 2300, а при Re > 104 устанавливается развитый турбулентный режим (здесь d — внутренний диаметр трубы).
Число Прандтля (1875—1953):
Pr = cρv/λ [115]
состоит из величин, характеризующих теплофизические свойства вещества и по существу само является теплофизической константой вещества. Значение числа Рг приводится в справочниках {15}.
В случае естественной конвекции скорость жидкости вдали от поверхности wж = 0 и соответственно Re = 0, но на теплоотдачу будет влиять подъемная сила Fп. Это приведет к появлению другого безразмерного параметра — числа Грасгофа:
Gr = gβ(tc-tж)/l3/ v2. [116]
Оно характеризует отношение подъемной силы, возникающей вследствие теплового расширения жидкости, к силам вязкости.
Дата добавления: 2014-12-24; просмотров: 1103;
