ЭНТРОПИЯ ГАЗОВ. TS -ДИАГРАММА
Для более полного исследования термодинамических процессов и облегчения исследований и расчетов в термодинамику был введен математически немецким физиком Р. Клаузиусом еще один параметр состояния газа (шестой) — энтропия S. Его название происходит от греческого слова превращение.
Энтропию измеряют в тех же единицах, что и массовую теплоемкость, т. е. в кДж/кг.град
| Сжатие Расширение |
(или при использовании внесистемной единицы ккал/кг.град). Энтропию обозначают буквой s для 1 кг газа и буквой S для G кг.
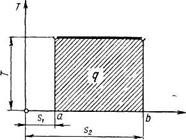 Рис.5 Изотермический процесс в TS-диаграмме
Рис.5 Изотермический процесс в TS-диаграмме
Таким образом, в термодинамике используются три основных параметра — р, vи Т (давление,удельный объем и температура) и три дополнительных — и, i и s (внутренняя энергия, энтальпия и энтропия).
 С точки зрения графического изображения энтропия как параметр состояния газа может быть использована в прямоугольной системе координат Ts, где в соответствующем масштабе s — энтропию — откладывают по оси абсцисс, а Т — абсолютную температуру — по оси ординат. Такая диаграмма в координатах Tsназывается Тs-диаграммой Т = const, линия процесса 1—2 (рис.6 ) будет проходить параллельно оси s. В таком случае площадь прямоугольника в некотором масштабе будет измерять количество тепла q, участвующего в изометрическом процессе, т. е. q = (s2 –s1)T, где s1 — энтропия 1 кг газа в начальном состоянии; s2 — энтропия 1 кг газа в конечном состоянии;
С точки зрения графического изображения энтропия как параметр состояния газа может быть использована в прямоугольной системе координат Ts, где в соответствующем масштабе s — энтропию — откладывают по оси абсцисс, а Т — абсолютную температуру — по оси ординат. Такая диаграмма в координатах Tsназывается Тs-диаграммой Т = const, линия процесса 1—2 (рис.6 ) будет проходить параллельно оси s. В таком случае площадь прямоугольника в некотором масштабе будет измерять количество тепла q, участвующего в изометрическом процессе, т. е. q = (s2 –s1)T, где s1 — энтропия 1 кг газа в начальном состоянии; s2 — энтропия 1 кг газа в конечном состоянии;
Отсюда следует, что s2 –s1 =  или
или 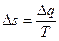
Рис.6 Количество тепла в TS-диаграмме
Таким образом, для графического изображения количества тепла в Ts-диаграмме пользуются двумя параметрами — энтропией и абсолютной температурой, при этом количество сообщенного или отнятого тепла, получаемого при произвольных изменениях состояния, выражается площадями диаграммы Ts подобно тому, как работа выражается площадями в PV-диаграмме. Отношение  Δq/T – (приведенная теплота) является качественной характеристикой процессов преобразования тепла.
Δq/T – (приведенная теплота) является качественной характеристикой процессов преобразования тепла.
Для изменения параметров идеального газа в равновесных процессах:
 [41]
[41]
Следовательно, под энтропией тела можно понимать величину, изменение которой Δs в любом элементарном термодинамическом процессе равно отношению внешнего тепла Δq, участвующего в этом процессе, к абсолютной температуре тела T.
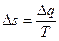 .
.
Энтропия является мерой потери работоспособности системы вследствие необратимости реальных процессов. Потеря работы от необратимого процесса прямо пропорциональна возрастанию энтропии.
Изменение энтропии, как и изменение внутренней энергии, энтальпии и некоторых других термодинамических величин не зависит от пути протекания процесса, а зависит лишь от начального и конечного состояний рабочего тела.
В уравнении  абсолютная температура Т — величина всегда положительная. Следовательно, Δq и Δs имеют одинаковые знаки, т. е. если Δq положительно, то и Δs положительно и, наоборот, если Δq отрицательно, то и Δs отрицательно. Таким образом, в обратимых процессах с подводом тепла (Δq >0) энтропия газа увеличивается, а в обратимых процессах с отводом тепла (Δq <0) энтропия газа уменьшается. Это важное свойство параметра s.
абсолютная температура Т — величина всегда положительная. Следовательно, Δq и Δs имеют одинаковые знаки, т. е. если Δq положительно, то и Δs положительно и, наоборот, если Δq отрицательно, то и Δs отрицательно. Таким образом, в обратимых процессах с подводом тепла (Δq >0) энтропия газа увеличивается, а в обратимых процессах с отводом тепла (Δq <0) энтропия газа уменьшается. Это важное свойство параметра s.
При температурах, близких к абсолютному нулю, все известные вещества находятся в конденсированном состоянии. В. Нернст (1906 г.) экспериментально установил, а М. Планк (1912 г.) окончательно сформулировал следующий принцип: при температуре, стремящейся к, абсолютному нулю, энтропия вещества, находящегося в конденсированном состоянии с упорядоченной кристаллической структурой, стремится к нулю, т.е. s0 = 0 (постоянная интегрирования) при T = 0К. Этот закон называют третьим законом термодинамики или тепловой теоремой Нернста. Он позволяет рассчитать абсолютное значение энтропии в отличие от внутренней энергии и энтальпии, которые всегда отсчитываются от произвольного уровня.
Получим формулы, позволяющие вычислять изменение энтропии идеального газа. Для этого проинтегрируем уравнение [41],
Например, для изохорного процесса при cυ = const, S2-S1 = cυ ln 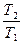 +R ln
+R ln 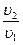
Из уравнения Клапейрона, записанного для состояний 1 и 2, следует:

 . После подстановки отношений Т2/Т1 и υ2/υ1 в полученное выражение получим следующие формулы для изменения энтропии идеального газа:
. После подстановки отношений Т2/Т1 и υ2/υ1 в полученное выражение получим следующие формулы для изменения энтропии идеального газа:
S2-S1 = cp ln( 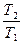 ) - R ln(
) - R ln( 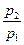 ); S2-S1 = cυ ln(
); S2-S1 = cυ ln( 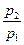 ) +cp ln(
) +cp ln( 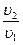 )
)
 Для адиабатного процесса, протекающего без теплообмена газа с внешней средой,
Для адиабатного процесса, протекающего без теплообмена газа с внешней средой,
s1 = s2 = s = const.
так как в этом процессе q = 0, то Δs = 0. Следовательно, адиабатный процесс в Ts-диаграмме изображается прямой вертикальной линией, перпендикулярной оси s. Для политропного процесса
где с — теплоемкость политропного процесса.
| рис. 7 Политропные процессы в TS -диаграмме |
S2-S1 = c ln 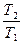
С позиций кинетической теории газов энтропию можно определить как меру неупорядоченности системы. Когда от системы при постоянном давлении отводится теплота, энтропия уменьшается, а упорядоченность в системе повышается. Это можно наглядно продемонстрировать на примере превращения газообразного вещества в твердое.
Молекулы газа движутся беспорядочно. Когда газ при отводе теплоты и соответствующем уменьшении энтропии конденсируется в жидкость, молекулы занимают более определенное положение (некоторое время молекула жидкости колеблется около какого-то положения равновесия, затем положение равновесия смещается и т. д., т. е. происходят одновременно медленные перемещения молекул и их колебания внутри малых объемов). При дальнейшем понижении температуры жидкости энтропия уменьшается, а тепловое движение молекул становится все менее интенсивным. Наконец, жидкость затвердевает, что связано с дальнейшим уменьшением энтропии, неупорядоченность становится еще меньше (молекулы только колеблются около средних равновесных положений.
Дата добавления: 2014-12-24; просмотров: 22340;
