Логарифмические частотные характеристики
В практических расчетах наряду с использованием АФЧХ широко используются так называемые логарифмические амплитудные фазовые частотные характеристики ЛАФЧХ или просто логарифмические частотные характеристики. При этом различают логарифмические амплитудные частотные характеристики ЛАЧХ и логарифмические фазовые частотные характеристики ЛФЧХ.
ЛАЧХ называют зависимость L(ω)=lgА(ω) от lg (w),
ЛФЧХ называют зависимость j(ω)от lg (w).
| 1 дек. |
w 
|
| х = lg(w) |
Рисунок 1.6 – Ось абсцисс
Интервал частот, кратный 10, называется декадой. Одна дек на чертежах равна 50 мм.
По оси ординат при построении ЛАЧХ откладывается величина L(w) в логарифмическом масштабе. Один лог на чертежах равен 50 мм.
Логарифм может быть разбит на более мелкие единицы
1 лог = 10 дл (децилог) = 20 дб (децибел), таким образом:
Y [дл] = 10 lg k,
Y [дб] = 20 lg k.
По оси ординат при построении ЛФЧХ откладывается величина j(w) в градусах, т.е. полулогарифмический масштаб. На чертежах отрезок 90° равен 45 мм.
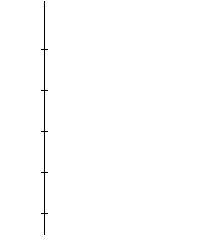
| L(w) |
| y = lg A(w) |
| 100 |
| 10 |
| 1 |
| 0,1 |
| 0,01 |
| лог. |
| 1 |
| -1 |
| 0 |
| 2 |
| -2 |
| дл. |
| 0 |
| 10 |
| -10 |
| 20 |
| -20 |
| дб. |
| 0 |
| 20 |
| -20 |
| 40 |
| -40 |
Рисунок 1.7 – Ось ординат
Достоинства ЛФЧХ:
1. При использовании ЛЧХ представляется возможным изображать величины, несоизмеримые в равномерном масштабе (например, от 0,01 до 1000).
2. При использовании ЛЧХ операция умножения коэффициентов усилительных звеньев заменяется операцией сложения ординат характеристик этих звеньев.
При использовании логарифмического масштаба нелинейные зависимости превращаются в прямые линии.
Дата добавления: 2014-12-22; просмотров: 723;
