Понятие о передаточной функции
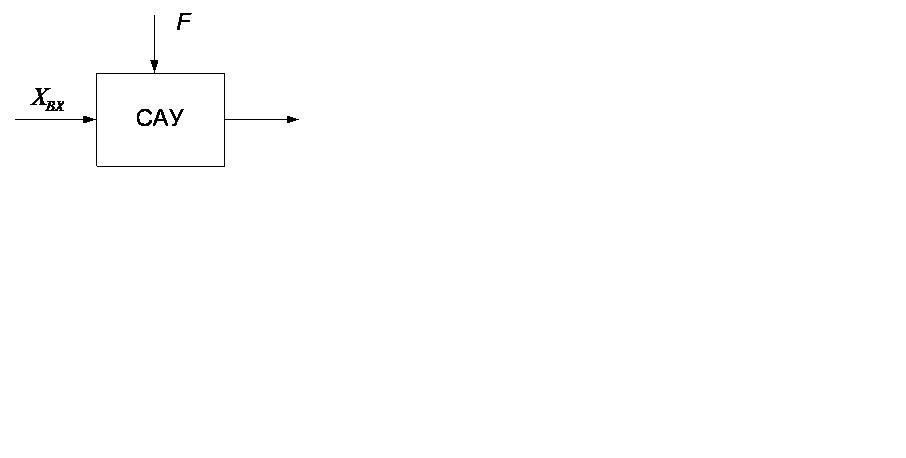
Если решать систему линеаризации дифференциальных уравнений, составленных для каждого элемента САУ относительно какой-либо одной регулируемой величины х(t)=хВЫХ(t) по отношению к отклонению
Рисунок 1.1 – Систем АУ х(t)=хВХ(t) и к возмущающему воздействию
f (t), то в результате получим дифференциальные уравнения с постоянными коэффициентами следующего вида:
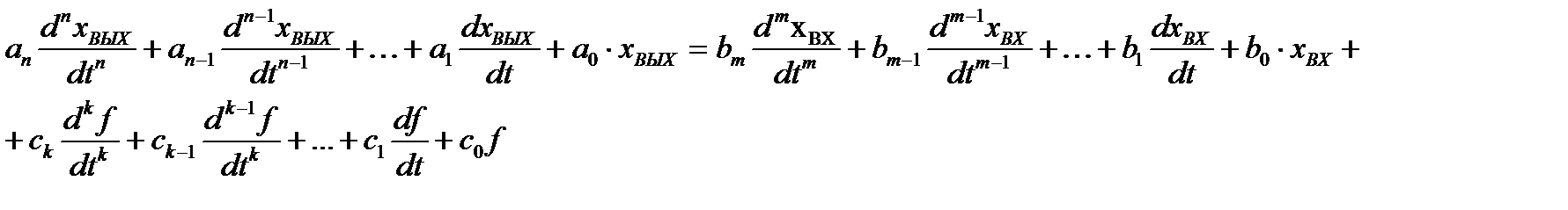, (1.1)
где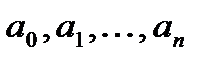 
; 
; 
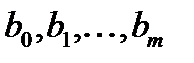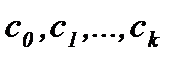- постоянные коэффициенты.
Уравнение (1.1) носит название общего дифференциального уравнения САУ или уравнения движения САУ.
Применяя к уравнению (1.1) при нулевых начальных условиях преобразование Лапласа, запишем это уравнение в операторной форме:
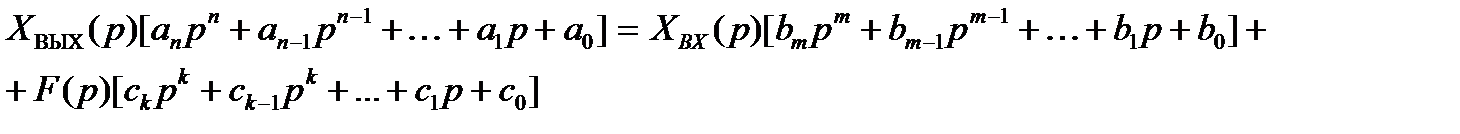, (1.2)
где XВЫХ(p); ХВХ(p) и F(p) – изображения соответственно функций xВЫХ(t); хВХ(t) и f(t).
Передаточной функцией САУ по задающему воздействию (рисунок 1.2,а) называется отношение операторного изображения выходной величины САУ к операторному изображению входной величины САУ при нулевых начальных условиях, т.е.:
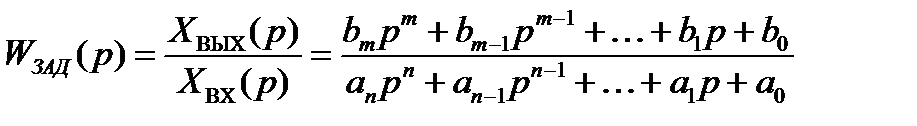. (1.3)
Соответственно, передаточной функцией САУ по возмущающему воздействию (рисунок 1.2,б) называют отношение операторного изображения выходной величины к операторному изображению возмущающего воздействия при нулевых начальных условиях
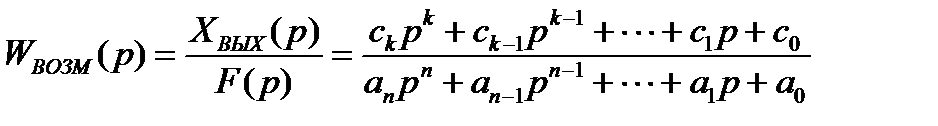. (1.4)
а) б)
Рисунок 1.2 – Передаточные функции
Т.к. при записи уравнений линейной САУ в операторной форме дифференциальные уравнения становятся алгебраическими, то с ними можно оперировать совершенно так же, как с линейными уравнениями для установившегося режима.
Обозначим соответственно
; 
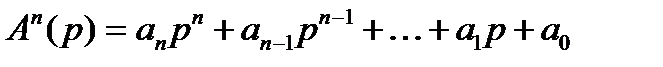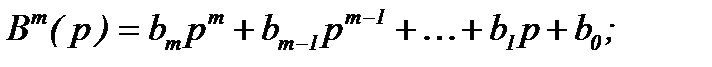- полиномы n-ой и m-ой степени от р.
Тогда передаточная функция по задающему воздействию равна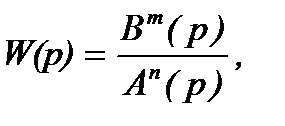 
(1.5)
где Аn(р)=0 – характеристическое уравнение.
Если известны полюсы рi и нули qi функции W(p), соответствующие корням An(p=0)и Bт(p)=0, то выражение (1.5) можно записать как
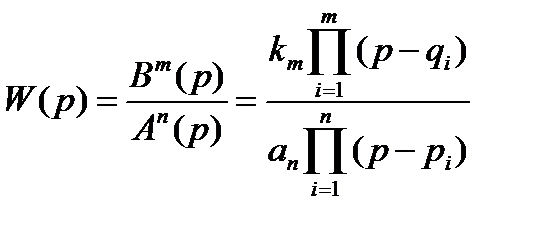. (1.6)
Предполагается, что полиномы An(p) и Bm(p) не имеют общих корней и дробь (1.6) не может быть сокращена.
Найдём переходную функцию при входном единичном ступенчатом воздействии
хВХ(t)=1(t) ,тогда ХВХ(р)= 
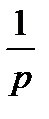. (1.7)
Вычислим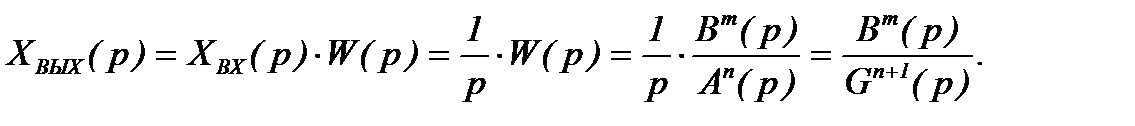 
(1.8)
Перейдём к оригиналу.
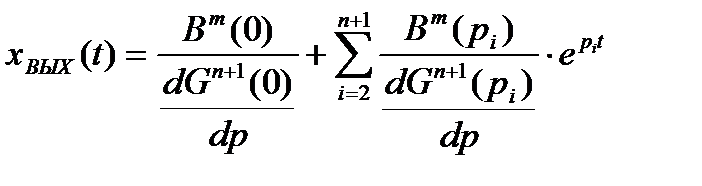, (1.9)
где рi – корни уравнения Gn+1(p)=0.
Здесь предполагается, что функция W(p) не имеет кратных полюсов и что n>m.
Дата добавления: 2014-12-22; просмотров: 1161;