Понятие о частотных характеристиках
Как известно, полное решение общего дифференциального уравнения САУ складывается из двух составляющих:
1. Свободной составляющей, которая находится из решения однородного дифференциального уравнения (характеристического уравнения)
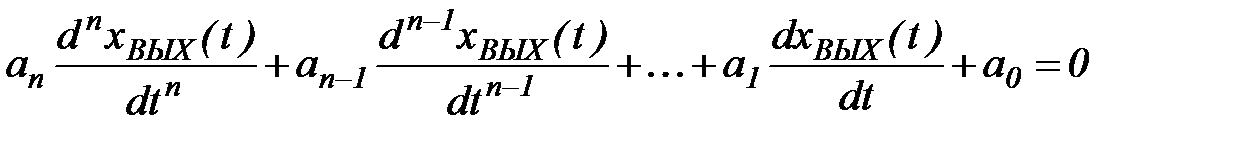 . (1.10)
. (1.10)
2. Вынужденной составляющей (частное решение), которая полностью определяется законом изменения во времени внешнего воздействия на САУ.
Удобно рассматривать динамику САУ (рисунок 1.1) или звена САУ при гармоническом изменении входной величины
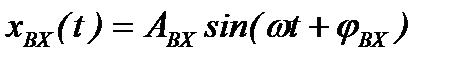 .
.
Тогда спустя некоторое время после начала действия XВХ на выходе системы установятся гармонические колебания той же частоты, что и частота входного воздействия, но имеющие другую амплитуду и фазу, т.е. вынужденную составляющую XВЫХ.
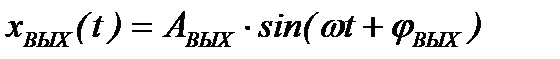
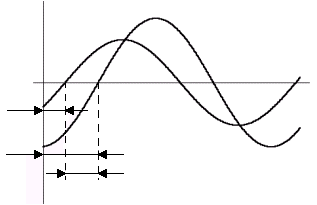
| хВЫХ |
| хВХ |
| jВХ |
| jВЫХ |
| j |
| wt |
Рисунок 1.3 – Входное и выходное значения
Очевидно, что при подаче на вход системы воздействия с той же амплитудой AВХ и начальной фазой jВХ, но другой частоты на выходе системы амплитуда AВЫХ и фаза jВЫХ будут иные.
Пример 1.1.
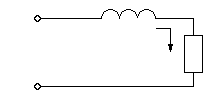
| u = Umsinwt |
| L |
| i |
| R |
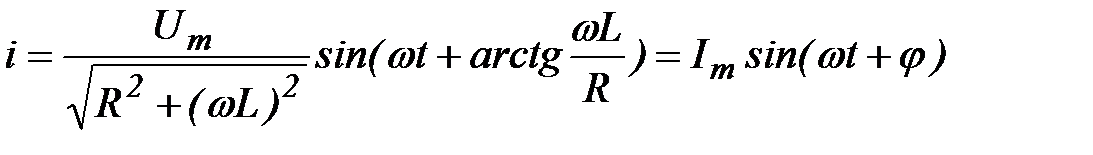
в данном случае Im и j являются функцией w.
Зависимость относительной амплитуды выходной величины от частоты называют амплитудно-частотной характеристикой (АЧХ) САУ
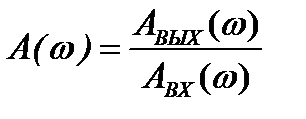 - АЧХ. (1.11)
- АЧХ. (1.11)
Зависимость сдвига фаз между гармоническими колебаниями выходной и входной величины от частоты называют фазо-частотной характеристикой (ФЧХ) САУ
| А, j |
| А(w) |
| j(w) |
| w |
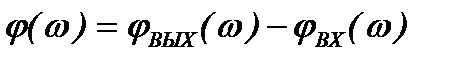 - ФЧХ . (1.12)
- ФЧХ . (1.12)
Рисунок 1.4 – Зависимость АЧХ и ФЧХ от частоты
Совместное изменение амплитуды и фазы выходной величины от частоты можно получить, если представить синусоидальные функции в комплексной форме:
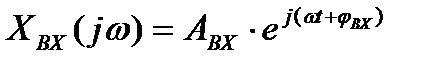 ,
,
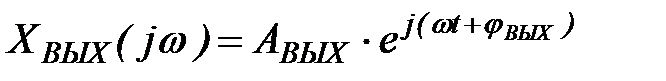 . (1.13)
. (1.13)
| АЧХ |
| ФЧХ |
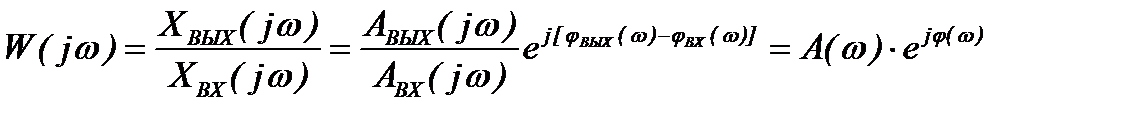 . (1.14)
. (1.14)
Комплексная функция W(jw) называется комплексным коэффициентом передачи САУ или амплитудно-фазовой частотной характеристикой (АФЧХ) САУ. Модуль этой функции представляет собой АЧХ, а аргумент – ФЧХ.
В общем случае W(jw) может быть представлен в виде числа
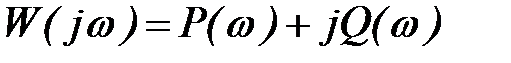 , (1.15)
, (1.15)
где P(w) – называется вещественной частотной характеристикой САУ (ВЧХ);
Q(w) – называется мнимой частотной характеристикой САУ (МЧХ).
Между собой ВЧХ, МЧХ и АЧХ, ФЧХ связаны
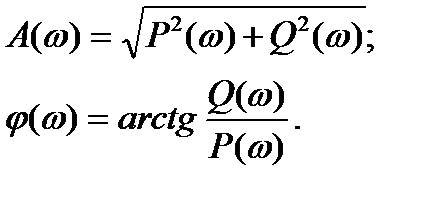
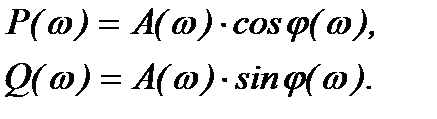 (1.16)
(1.16)
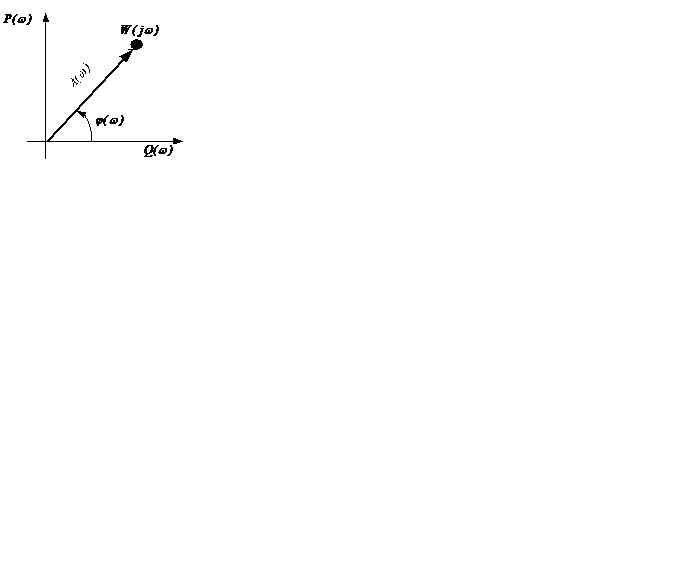 График
График 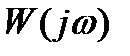 называется годографом - год
называется годографом - год 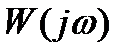 =
= 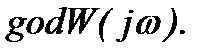
АФЧХ тесно связана с передаточной функцией САУ. При синтезе и анализе систем используются частотные методы, для этого к уравнению (1.1) следует применить преобразование Фурье. Для получения АФЧХ расчетным путем необходимо в передаточной функции звена или САУ положить Рисунок 1.5 – АЧХ, ФЧХ и p = jw.
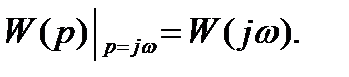 ВЧХ,МЧХ
ВЧХ,МЧХ
Пример 1.2.
Для функции 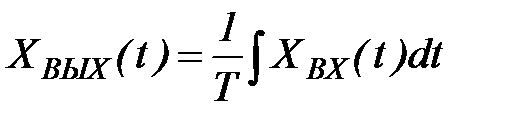 ,
, 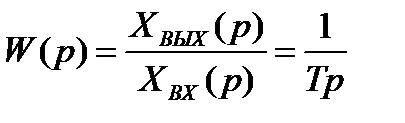 ,
,
должно быть 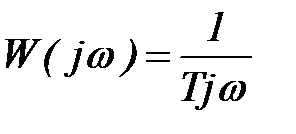 .
.
Пусть входная величина изменяется по синусоидальному закону, тогда:
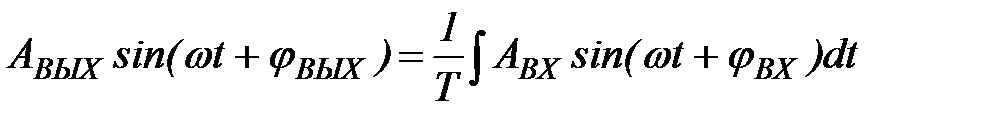 , (1.17)
, (1.17)
или в комплексной форме
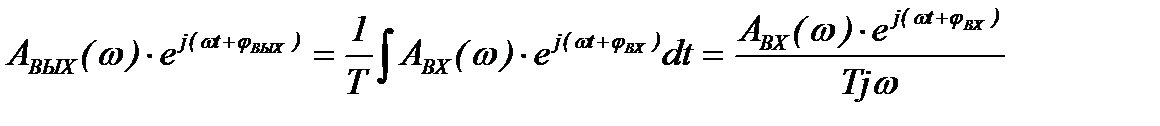 , (1.18)
, (1.18)
тогда
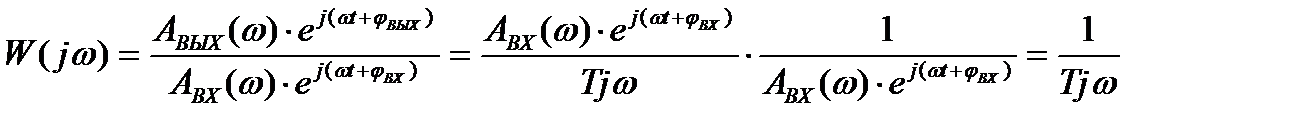 .
.
(1.19)
Таким образом, действительно АФЧХ получилась из передаточной функции заменой p = jw, в общем случае можно записать:
W(jw) = [W(p)]р = jw. (1.20)
Дата добавления: 2014-12-22; просмотров: 1093;
