Связи и их реакции. Принцип освобождаемости от связей

Тело называется свободным, если его перемещения ничем не ограничены. Тело, перемещение которого ограничено другими телами, называется несвободным. Тела, ограничивающие перемещения данного тела, называются связями. Силы, с которыми связи действуют на данное тело, называются реакциями связей.

Принцип освобождаемости: всякое несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к телу.

Основные типы связей:

а) опора на идеально гладкую поверхность – реакция поверхности направлена по нормали к ней, т.е. перпендикулярно касательной – нормальная реакция;

б) одна из соприкасающихся поверхностей является точкой (угол), реакция направлена по нормали к другой поверхности;

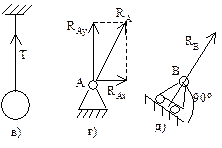в) нить – реакция направлена вдоль нити к точке подвеса;

г) цилиндрический шарнир (шарнирно-неподвижная опора) – реакция может иметь любое направление в плоскости, при решении задач заменяется двумя взаимно перпендикулярными составляющими;

д) цилиндрическая шарнирно-подвижная опора (шарнир на катках) – реакция направлена перпендикулярно опорной плоскости;

е) невесомый стержень (обязательно невесомый) – реакция направлена вдоль стержня;

ж) жёсткая заделка (заделанная в стену балка) – возникает произвольно направленная реакция – сила и реактивный момент, также неизвестный по направлению. Реакция раскладывается на две составляющие.

3. Проекция силы на ось и плоскость

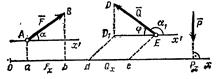Проекция силы на ось есть алгебраическая величина, равная произведению модуля силы на косинус угла между силой и положительным направлением оси. Если этот угол острый, проекция положительна, если тупой — отрицательна, а если сила перпендикулярна оси, ее проекция на ось равна нулю.

, , .

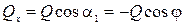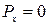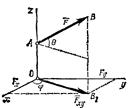Проекцией силы на плоскость Оху называется вектор , заключенный между проекциями начала и конца силы на эту плоскость. .

, ,

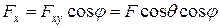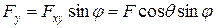Силы можно задавать не только при помощи векторов, но и аналитический, с помощью проекций силы на координатные оси. Пользуемся правой системой координат, т.е. такой, в которой кратчайшее совмещение оси Ox c Oy происходит, если смотреть с положительного конца оси Oz, против хода часовой стрелки.

Для пространственной системы: ,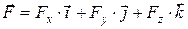

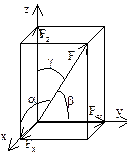F_x=Fcosa; F_y=Fcosb; F_z=Fcosg;

;

.

4. Сложение сил

Геометрический способ сложения сил

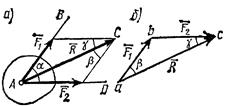1. Сложение двух сил.

Геометрическая сумма 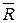двух сил 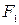и 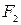находится по правилу параллелограмма или построением силового треугольника изображающего одну из половин этого параллелограмма.

,

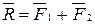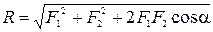
2. Сложение трех сил, не лежащих в одной плоскости.

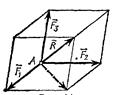
Геометрическая сумма 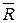трех сил , , 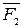, 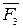не лежащих в одной плоскости, изображается диагональю параллелепипеда, построенного на этих силах (правило параллелепипеда). В справедливости этого убеждаемся, применяя последовательно правило параллелограмма.

3. Сложение системы сил.

Геометрическая сумма (главный вектор) любой системы сил определяется или последовательным сложением сил системы по правилу параллелограмма, или построением силового многоугольника. Второй способ является более простым и удобным. Для нахождения этим способом суммы сил , , 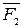, 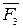…, , 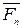откладываем от произвольной точки 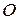вектор 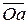, изображающий в выбранном масштабе силу 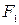, от точки 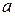— вектор 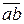изображающий силу 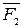, от точки 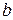— вектор 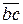, изображающий силу 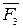, и т. д.; от конца предпоследнего вектора откладываем вектор , изображающий 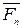. Соединяя начало первого вектора с концом последнего, получаем вектор 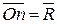изображающий геометрическую сумму или главный вектор слагаемых сил: .

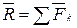Аналитический способ сложения сил.

Силы можно складывать и аналитически с помощью проекций этих сил на координатные оси. При этом проекция вектора суммы на какую-нибудь ось равна алгебраической сумме проекций слагаемых на ту же ось. 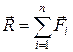-> R_x=åF_ix; R_y=åF_iy; R_z=åF_iz; .

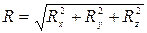Если силы расположены в одной плоскости, то R_x=åF_ix; R_y=åF_iy; .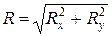

5. Равновесие системы сходящихся сил

Сходящимися называются силы, линии действия которых пересекаются в одной точке. Равнодействующая сходящихся сил равна геометрической сумме (главному вектору) этих сил и приложена в точке их пересечения 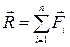. Для равновесия системы сходящихся сил, приложенных к твердому телу, необходимо и достаточно, чтобы равнодействующая этих сил были равны нулю

1. Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный из этих сил, был замкнутым.

2. Аналитические условия равновесия. 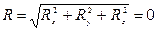ó , , .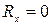

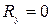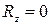Следовательно, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю. åF_ix=0; åF_iy=0; åF_iz=0.Для плоской системы только первые 2 уравнения.

3. Теорема о трех силах: Если твердое тело находится в равновесии под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

Для доказательства теоремы рассмотрим сначала какие-нибудь 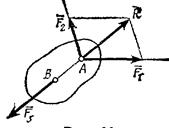две из действующих на тело сил, например и . Так как по условиям теоремы эти силы лежат в одной плоскости и не параллельны, то их линии действия пересекаются в некоторой точке А. Приложим силы и в этой точке и заменим их равнодействующей . Тогда на тело будут действовать две силы: сила 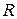и сила 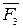, приложенная в какой-то точке В тела. Если тело при этом находится в равновесии, то силы 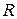и сила 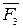, должны быть направлены по одной прямой, т.е. вдоль АВ. Следовательно, линия действия силы 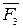тоже проходит через точку А, что и требовалось доказать.

Обратное утверждение места не имеет, т. е. если линии действия трех сил пересекаются в одной точке, то тело под действием этих сил может и не находиться в равновесии; следовательно, теорема выражает только необходимое условие равновесия тела под действием трех сил.