Теоретична і дійсна зрівноваженість двигуна

Під час виведення умов зрівноваженості вважалось, що маси рухомих деталей всіх циліндрів абсолютно однакові, величини R, l і кути розташування всіх колін абсолютно рівні, густина металу стала та кутові швидкості різних колін також рівні. Проте не враховувались сили інерції вищих порядків.

У дійсності згідно технологічних причин розміри і маси деталей двигуна завжди відрізняються від номінальних значень. Крім того, ці деталі, а саме, колінчастий вал, не є абсолютно жорсткими і деформуються під впливом сил, що на них діють.

Внаслідок вказаних вище причин дійсна зрівноваженість двигуна буде значно нижча за теоретично можливу. Для зменшення цієї різниці деталі, що обертаються ретельно балансують, а деталі, що рухаються зворотно-поступально підбирають таким чином, щоб у одному двигуні були деталі з найменшими відхиленнями в масі.

Колінчасті вали, маховики і зчеплення автомобільних і тракторних двигунів балансують. Під час такого балансування деталь обертають. Якщо деталь незрівноважена, то відцентрові сили незрівноважених мас спричиняють коливання пружної рами балансувальної установки. Амплітуди цих коливань характеризують ступінь незрівноваженості деталі.

На даний час на вітчизняних заводах динамічне балансування деталей здійснюють на спеціальних машинах, що дозволяють визначити величину і площину дії незрівноваженого моменту.

Допустимий дисбаланс досягається видаленням у певному місці надлишкового металу висвердлюванням, або іншим способом.

Для усунення незрівноваженості, що залежить від неоднакових мас деталей, які рухаються зворотно-поступально, поршні та хитні під час складання старанно підбирають за вагою. Звичайно поршні та хитні розбивають на групи з невеликим допуском за вагою для кожної групи (1...5 г). Варто відмітити, що хитні перевіряють не тільки за вагою, але і за положенням центра ваги хитня, а також і за величиною його моменту інерції.

Недотримання технічних умов на обробку деталей двигуна може привести до виникнення значних незрівноважених сил інерції.

Дійсна зрівноваженість двигуна відрізняється від теоретичної, і внаслідок того, кутова швидкість w обертання колінчастого валу двигуна не є постійною величиною, так як це було прийнято під час дослідження кінематики і динаміки хитневого механізму, а періодично змінюється в часі. Періодом зміни кутової швидкості w є період робочого процесу двигуна, тобто два оберти колінчастого валу для чотиритактних двигунів і один оберт – для двотактних.

Несталість кутової швидкості w є наслідком і крутильних коливань системи колінчастого валу, що виникають внаслідок недостатньої його жорсткості під дією періодично змінних обертальних моментів двигуна. Період зміни цих моментів той, що і період зміни кутової швидкості w, тобто два оберти колінчастого валу для чотиритактних і один оберт – для двотактних двигунів.

Кутова швидкість w, як і будь-яка періодична функція, що задовольняє умовам Діріхле, може бути представлена у формі ряду Фур’є. У цьому випадку закон зміни кута j повороту колінчастого валу можна виразити з достатньою точністю рівнянням

,

де 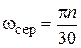– середня кутова швидкість обертання колінчастого валу; t – час, що відповідає куту повороту колінчастого валу на кут j; n – кількість обертів колінчастого валу; k= 1, 2, 3, 4,... – порядок гармоніки; 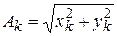– амплітуда гармоніки k-го порядку; x_k, y_k – амплітуди фазових складових гармонік k-го порядку; a_k – початковий фазовий кут, що визначається з виразу

.

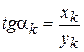Значення величини A_k і a_k для різних колін валу неоднакові. Внаслідок цього закон зміни кута j та кутової швидкості w, що має місце під час крутильних коливань системи колінчастого валу також неоднакові.

Оскільки сили інерції першого F_j1, другого F_j2 порядків, відцентрові сили інерції F_c та моменти від цих сил T_j1, T_j2, T_c пропорційні квадрату кутової швидкості w², що неоднакова у разі крутильних коливань в певний момент часу для різних колін валу, зрівноваженість двигуна порушується.

Умови Діріхле формуються наступним чином:

1) функція f(x) у проміжку аргументу від x= –p до x= +p повинна мати скінчене число максимумів та мінімумів;

2) у разі деяких часткових значень x=x_i (кількість цих значень повинно бути скінченим) функція f(x) може мати розриви неперервності першого порядку, тобто такі розриви, за яких для даної точки функція прямує до певних скінчених границь, що відмінні одна від одної (в залежності від того, чи наближається x до даної точки збільшуючись чи зменшуючись);

3) граничні значення функції, тобто значення f(–p+0) і f(+p–0) повинні бути скінченими і рівні, або нерівні між собою.