Розрахунок деталей двигуна з врахуванням змінного навантаження
В автомобільних двигунах навіть у випадку усталеного режиму роботи більшість деталей працює в умовах змінних навантажень. Внаслідок цього вплив максимальних навантажень і характер їх дії у випадку зміни в часі суттєво впливає на працездатність деталей. Тому, відповідальні деталі двигуна розраховують як на статичну міцність від дії максимальної сили, так і на втомну міцність від дії змінних навантажень.
З опору матеріалів відомо, що змінне навантаження викликає зміну напруження циклічного характеру, причому цикли можуть бути симетричними, асиметричними та пульсуючими. Тому для циклу характерні такі значення напружень: smax, smin, tmax і tmin, середні значення 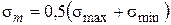 або
або 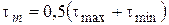 , амплітуда циклу
, амплітуда циклу 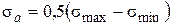 або
або 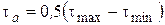 , коефіцієнт асиметрії
, коефіцієнт асиметрії 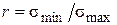 , який для симетричного циклу r = –1, для пульсуючого r = 0.
, який для симетричного циклу r = –1, для пульсуючого r = 0.
У випадку статичних навантажень за граничне приймають значення межі міцності sв чи межі текучості sТ. У випадку змінних навантажень за небезпечне напруження приймають межу втоми sr або межу текучості sТ.
Якщо нормальні чи дотичні напруження відповідають умові
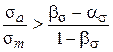 або або 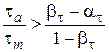 , ,
| (2.1) |
розрахунок проводять за межею втоми sr. У іншому випадку – за межею текучості sТ.
У виразах (2.1) величини bs і bt – це відношення межі втоми під час згину (розтягу-стиску) чи крученні до границі текучості:
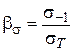 і
і 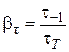 ,
,
де as і at –коефіцієнти приведення асиметричного циклу до рівноцінного симетричного відповідно для нормальних і дотичних напружень. Значення as і at для сталей з різними значеннями меж міцності наведено в табл. ІI.1 додатку IІ.
У випадку відсутності даних для вирішення рівнянь (2.1) запас міцності деталі визначають і за межею втоми, і за межею текучості. З двох отриманих значень міцність оцінюють за меншим коефіцієнтом.
Запас міцності без врахування форми, розмірів та обробки деталі визначають за формулами:
за межею втоми
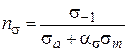 , , 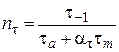 ; ;
| (2.2) |
за межею текучості
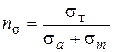 , , 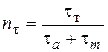 . .
| (2.3) |
Вплив на втомну міцність деталі враховують наступними величинами:
1) коефіцієнтами концентрації напружень: теоретичним aкs і ефективним ks (kt), який враховує підвищення напруження у зв’язку зі зміною форми деталі;
2) масштабним коефіцієнтом eм, що враховує вплив абсолютних розмірів деталі на межу втоми;
3) коефіцієнтом поверхневої чутливості eп, що враховує вплив стану поверхні деталі на межу міцності.
Теоретичний коефіцієнт концентрації напружень aкs для найбільш розповсюджених концентраторів наведено в табл. ІI.6. додатку ІI.
Ефективний коефіцієнт концентрації напружень ks знаходять із залежності
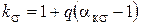 , ,
| (2.4) |
де q – коефіцієнт чутливості матеріалу (для чавуну q = 0; для конструкційних сталей – q = 0,6...0,8; для високоміцних сталей – q = 1). Коефіцієнт q залежно від aкs і межі міцності sв точніше можна визначити з номограм (рис. 75 [11]).
У випадку відсутності в деталі різких переходів і за якісної обробки поверхні єдиним фактором, що викликає концентрацію напружень, є якість внутрішньої структури матеріалу. В цьому випадку ефективний коефіцієнт концентрації напружень знаходять із залежності
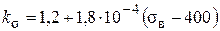 , ,
| (2.5) |
де sв – межа міцності матеріалу.
Зв’язок між коефіцієнтами ks і kt виражається залежністю
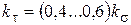 . .
| (2.6) |
Масштабним коефіцієнтом називають відношення межі втоми зразка діаметром d до межі втоми стандартного зразка (dст = 10 мм). Значення коефіцієнта eм для конструкційних сталей наведено в табл. ІI.5. додатку ІI.
Коефіцієнтом поверхневої чутливості називається відношення межі втоми зразка із заданим станом поверхні до межі втоми такого ж зразка, але з полірованою поверхнею. Значення коефіцієнта eп для різних станів поверхні наведено в табл. ІI.7. додатку IІ.
Для підвищення втомної міцності рекомендується висока чистота поверхні, особливо поблизу концентраторів. Відповідальні деталі, що працюють у важких умовах циклічних напружень, здебільшого шліфують і полірують, а в деяких випадках виконують механічне або термічне зміцнення.
З врахуванням впливу концентраторів розмірів і обробки поверхні максимальне напруження циклу:
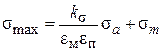 , ,
| (2.7) | |
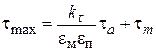 . .
| (2.8) |
Запас міцності за межею втоми знаходимо за формулою
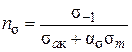 , , 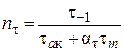 ; ;
| (2.9) |
Запас міцності за межею текучості знаходимо за формулою
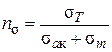 , , 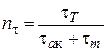 , ,
| (2.10) |
де 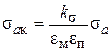 і
і 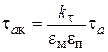 .
.
У випадку складного навантаження загальний запас міцності деталі за одночасної дії на неї дотичних і нормальних напружень
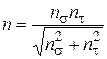 , ,
| (2.11) |
Дата добавления: 2014-12-22; просмотров: 1149;
