Поправка компаса и способы ее определения 4 страница

Точные значения Δ 1' (мм) даются в Картографических таблицах. Главный масштаб на проекции Меркатора относится только к главной параллели, и этот масштаб (численный) указывается в заголовке карты. Кроме того, на картах указывается масштаб по экватору. Главной может быть любая параллель, в том числе и экватор. В последнем случае цилиндр будет касаться земного эллипсоида (шара) по линии экватора. Во всех остальных случаях цилиндр будет секущим и главной параллелью проекции будут параллели сечения эллипсоида цилиндром.
Масштаб в проекции Меркатора, оставаясь постоянным по всем направлениям в любой точке, меняется от точки к точке с изменением широты. На главной параллели увеличение масштаба равно единице и искажения длин отсутствуют. Частный масштаб в любой точке карты равен увеличению масштаба. Чтобы установить зависимость масштаба на проекции Меркатора от широты, найдем отношение масштабов в двух точках проекции, расположенных на разных параллелях φ₁ и φ₂.
Масштабы в каждой из этих точек по всем направлениям одинаковы. Поэтому сравнивать можно любые частные масштабы в этих точках по параллелям или по меридианам.

Рассмотрим отношение масштабов по параллелям. Будем при этом считать, что экватор является главной параллелью, следовательно, масштаб по экватору равен главному масштабу и увеличение масштаба на экваторе равно единице.
Масштаб проекции в точке А' на параллели φ₁ (рисунок) равен

n₁ = A'B' / A'_oB'_o = adλ / r₁dλ = a / N₁ cos λ₁,

где adλ —длина изображения отрезка параллели на проекции между заданными меридианами, равная длине отрезка экватора между теми же меридианами, так как по свойству проекции каждая параллель на проекции увеличивается или уменьшается до длины главной параллели;
r₁dλ — длина отрезка параллели между заданными меридианами на условном глобусе.

Из приведенной формулы видно, что вдоль параллели масштаб изображения изменяться не будет, так как величины а, r₁, φ₁ остаются неизменными. Следовательно, параллели в проекции Меркатора являются линиями постоянного масштаба. С изменением широты радиус параллели меняется, уменьшаясь с увеличением φ, величина а при этом остается неизменной. Уменьшение знаменателя дроби приводит к увеличению частного, т. е. к увеличению масштаба с возрастанием широты.

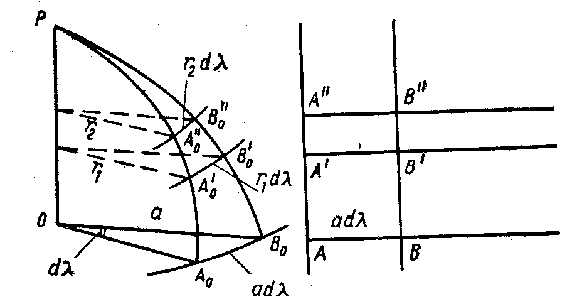
По аналогии с предыдущим получим масштаб для точки А" на параллели φ₂

n₂ = A''B'' / A''_oB''_o = adλ / r₂dλ = a / N₂cos φ₂

Сравним полученные масштабы в точках А' и А", взяв их отношение

n₂ / n₁ = a / N₂cos φ₂ :
N₁cos φ₁ / N₂cos φ₂

Без учета сжатия Земли аналогичное отношение масштабов на разных параллелях будет иметь вид

n₂ / n₁ = cos φ₁ / cos φ₂

Таким образом, показано, что с увеличением широты масштаб на проекции Меркатора увеличивается. Формулы (94) и (95) позволяют определить масштаб или увеличение масштаба на любой параллели, если известно увеличение масштаба на одной из них.
Так как в заголовке карты всегда приводится масштаб n_о для главной параллели (φ_o), то при возникновении необходимости вычислить масштаб в любой точке проекции на параллели φ₁ можно воспользоваться формулой

n₁ / n_o = N_o cos φ_o / N₁ cos φ₁ (96)

с учетом сжатия Земли или формулой
n₁ / n_o = cos φ_o / cos φ₁ (97) без учета сжатия Земли.

Если в формулах (96), (97) от масштабов n₁ и n_o перейти к знаменателям числовых масштабов С₁ и С_о, то они примут вид:

— с учетом сжатия Земли (98)

C_o / C₁ = N_ocos φ_o / N₁cos φ₁,

- без учета сжатия Земли (99)

C_o / C₁ = cos φ_o / cos φ₁.

Полученные формулы выражают так называемый модуль параллели Ø —число, разделив на которое знаменатель главного масштаба, получают знаменатель частного масштаба на любой другой параллели.

Из определения следует, что C = C_o / Ø, откуда

Ø = C_o / C = N_o cos φ_o / N cos φ = r_o / r = r_o arc 1' / r arc 1' . (100)

Модуль параллели Ø легко вычислить по любому из последних равенств. В приведенных равенствах использована величина r arc 1' = P, которая представляет собой длину одной минуты дуги параллели в мм. Величины P для широт от 0 до 89° 55' приводятся в Картографических таблицах.
Таким образом, модуль параллели V можно вычислить с помощью Картографических таблиц по формуле Ø = P_o / P, а в случае отсутствия таблиц рассчитать по формуле

Ø = N_o cos φ_o / N cos φ = r_o

или, если принимать Землю за шар,

Ø = cos φ_o / cos φ. (101)

Пример.
Требуется рассчитать частный масштаб карты в проекции Меркатора по параллели с широтой φ = 56°N, если главный масштаб по параллели с широтой φ_o = 60° N равен µ_o = 1 : C_o = 1:200000.

Решение.
1. Из Картографических таблиц выбираем Р_о = P₆₀ =930015 мм и P₅₆ = 1039897 мм.
2. Модуль параллели Ø для широты φ = 56° равен

Ø = P_o / P = 930015 / 1039897 = 0, 89424.

3. Знаменатель частного масштаба для параллели φ =56° N равен С = Со: Ø = 200000 : 0,89424 = 223630, а искомый масштаб будет µ = 1 : 223630.

Полосы широт практически постоянного масштаба.

Длина меркаторской мили с увеличением широты непрерывно возрастает. При пользовании картой это обстоятельство принимается во внимание и отрезки длин — расстояний на карте в проекции Меркатора — измеряются той частью линейного (широтного) масштаба, который расположен около средней параллели измеряемого отрезка. При построении линейного (широтного) масштаба вертикальную рамку нужно разбить на отрезки, равные меркаторской миле, имеющей в различных широтах разную длину. Наиболее строгим и точным решением такой задачи был бы расчет картографических абсцисс x = f (φ) для всех параллелей от широты южной рамки до широты северной рамки карты с широтным интервалом в одну минуту. Однако такой расчет является чрезвычайно сложным и трудоемким. Этого и не требуется для практических задач. Поэтому при составлении карты параллели проводятся через определенные промежутки (широтный интервал) Δ φ, внутри которых деление рамки на минуты осуществляется разбивкой их на равные части, соответствующие средней длине меркаторской мили в данном промежутке. Внутри такой полосы широт Δ φ изменение масштаба настолько мало, что оно не превышает ошибок графических построений. Какова же та разность широт, в пределах которой длина меркаторской мили без ущерба для точности графических построений может быть принята постоянной величиной.
Проведенное профессором В. В. Каврайским исследование позволило установить зависимость полосы широт практически постоянного масштаба от широты и масштаба карты. Эта зависимость выражена следующей формулой:

Δφ' = √ {(C_Nctg φ_N) / 675} или

Δφ' = √ { (C₁ ctg φ₁) / 675} (102)

где C₁ — знаменатель частного масштаба на рамке карты в широте φ₁;
φ₁ — широта ближайшей к полюсу рамки карты.

В готовом виде величины промежутков практически постоянного масштаба приводятся в Картографических таблицах. Рассчитанный (или выбранный из таблиц) промежуток практически постоянного масштаба округляется в меньшую сторону до значения, кратного 5' или 10', и принимается затем в качестве широтного интервала, через который на карте проводятся параллели картографической сетки. Если выбранный или рассчитанный широтный интервал окажется меньше 5', то округление производится также в меньшую сторону до значения, кратного одной целой минуте.

Пример.
Рассчитать величину широтного интервала, через который должны быть проведены на карте параллели, чтобы в промежутках между ними меркаторскую милю можно было считать величиной постоянной. Масштаб карты 1 :300 000 по главной параллели 60° и район картографируемой местности ограничен параллелями φ_S = 59° N и φ_N = 62°30' N.

Решение.
1. По формулам C_N = C_o / Ø и Ø = P_o / P_N находим C_N.
P_o = 930015, lg P_o = 5,96849.
P_N = 858973, lg P_N = 5,93398/
lg Ø = 0, 03451
C_o = 300000, lg C_o = 5,47712
lg C_N = 5,44261
C_N = 277080.

2. По формуле Δ φ' = √ { (C_Nctg φ_N) / 675} находим Δ φ'.
C_N = 277080, lg C_N = 5,44261
φ_N = 62° 30', lg ctg φ_N = 9,71648
Σ = 5,15909
lg 675 = 2,82930
2 lg Δ φ' = 2,32979
lg Δ φ' = 1,16489
Δ φ' = 14,6'.
Округляя полученный интервал Δ φ' в меньшую сторону, принимаем Δ φ' = 10'.