Поправка компаса и способы ее определения 2 страница
Δл% = {S - (ол2 - ол1) / (ол2 - ол1)} * 100 = {(S - рол) / рол} * 100
где S — расстояние, пройденное кораблем относительно воды;
рол = ол2 — ол1 — разность отсчетов лага, соответствующая расстоянию S.
Из формулы (41) следует, что расстояние S, проходимое кораблем относительно воды и определяемое на основании показаний лага с учетом его поправки, нужно вычислять по формуле
S = рол (1+ Δл% / 100) =рол * кл (42)
Выражение (1+ Δл% / 100) называется коэффициентом лага и обозначается кл. Поправка лага Δл может иметь знак плюс или минус. Если лаг отсчитывает расстояния меньше действительно проходимых кораблем, то поправка лага имеет знак плюс, и наоборот, когда лаг показывает расстояние больше проходимого кораблём в действительности, поправка лага имеет знак минус. При положительной поправке лага коэффициент лага всегда больше единицы, при отрицательной поправке лага коэффициент лага меньше единицы. Связь коэффициента лага с поправкой лага может быть выражена формулами 43:
кл = 1 + Δл% / 100
Δл% = 100 * (кл - 1)
Вместо вычислений пройденного расстояния S по формуле (42) можно пользоваться специальными таблицами 28-а, 28-б, помещенными в МТ. Табл. 28-а пользуются при положительных поправках лага, а табл. 28-б — при отрицательных. Аргументами для входа в таблицы служат разность отсчетов лага (она приведена в левом вертикальном столбце) и поправка или коэффициент лага, показанные в верхней горизонтальной строке. Пройденное расстояние S выбирается из таблицы на пересечении столбца и строки, соответствующих заданным значениям аргументов (рол, Δл, кл).
В тех случаях, когда разность отсчетов лага рол превышает 100 миль, ее разбивают на две (или несколько) произвольные части, в сумме дающие заданную разность отсчетов лага, но каждая из которых не превышает 100 миль. Выбрав из таблицы на каждую из частей аргумента пройденное расстояние и сложив их вместе, получают пройденное кораблем расстояние, соответствующее полному аргументу рол.
Пример 1. ол1 = 122,0 мили, ол2 = 248,0 мили, Δл = + 4%. Определить пройденное расстояние.
Решение. рол = ол2 - ол1 = 126,0 миль.
Разбив произвольно 126,0 миль на две части, например 90,0 миль и 36,0 миль, выбираем из табл. 28-а:
S1 = 90 * (1 + Δл% / 100) = 93,6 мили;
S2 = 36 * (1 + Δл% / 100) = 37,4 мили
и находим пройденное расстояние как сумму
S = S1 + S2 = 93,6 + 37,4 = 131,0 мили.
При поправке лага, превышающей 10%, ее разбивают на две части — Δ л1% и Δ л2% , каждая из которых меньше 10%, а сумма их равна заданной Δ л %. Пройденное расстояние при этом на основании формулы (42) можно определить по формуле
S = (ол2 - ол1)(1+ Δл1% / 100 + Δл2% / 100),
которая после преобразования принимает вид
S = (ол2 - ол1)(1 + Δл1% / 100) +
ол2 - ол1)(1 + Δл2% / 100) - (ол2 - ол1) (44)
или
S = рол * кл1 + рол * кл2 - рол
Для нахождения пройденного расстояния при разделении Δ л % или кл на две части нужно выбрать из таблицы исправленные расстояния по разности отсчетов лага для каждой из частей, сложить ИХ и из суммы вычесть разность, отсчетов лага. Значительно проще и быстрее, чем по таблицам 28-а, 28-6, исправление разности показаний лага его поправкой, выраженной в виде коэффициента лага кл можно производить с помощью логарифмической линейки. При этом задача сводится к умножению по линейке разности отсчетов лага (ол2 - ол1) на коэффициент лага кл в соответствии с формулой (42).
При решении некоторых задач навигации возникает необходимость заранее предвычислять показания лага (отсчеты лага) на заданный момент времени или для определенных точек на линии пути корабля, например для точек поворота на новый курс. В таких случаях по известному плаванию (расстоянию) до заданной точки и известной поправке лага можно рассчитать разность отсчетов лага по одной из следующих формул, полученных из (42):
(ол2 - ол1) = S / (1 + Δ л% / 100)
рол = S / кл (45)
Искомая разность отсчетов лага соответствии с формулами (45) может быть также получена обратным входом по таблицам 28-а и 28-6 МТ-63 или с помощью логарифмической линейки.
Прибавив вычисленную разность отсчетов лага (ол2 - ол1) к начальному отсчету ол1, получают предвычисленный отсчет лага ол2 на заданный момент.
Пример 2. Расстояние от некоторого исходного места до заданной точки, снятое с карты, равно 44,0 мили, Δ л = — 5%; начальный отсчет лага в исходной точке ол1 =16,8 мили. Найти отсчет лага ол2, который будет на счетчике лага в заданной точке.
Решение.
По формулам рол = ол2 — ол1 = S / кл и
кл = 1 + Δ л% / 100 = 0,95 с применением таблиц или логарифмической линейки находим:
ол2 — ол1 = 44 / 0,95 = 46,3 мили;
ол2 = ол1 + рол = 16,8 + 46,3 = 63,1 мили.
Поправка лага изменяется по величине и знаку с изменением скорости хода корабля. У исправного и хорошо отрегулированного лага поправка обычно невелика (до ±1%). Для регулировки лага и определения его поправки обычно используют выход корабля на мерную линию и производят эту работу одновременно с определением скоростей хода.
В одном из способов определения поправки лага производят сравнение действительно пройденного кораблем расстояния S между секущими створами мерной линии с расстоянием, полученным по показаниям лага. Расстояние, рассчитываемое при этом по показаниям лага, получают как разность отсчетов (ол2 — ол1), соответствующих моментам начала ол1 и окончания ол2 прохождения кораблем известного по длине отрезка S между двумя парами секущих створов. Затем по формуле
Δ л = {S - (ол2 — ол1)} / (ол2 — ол1) (46)
рассчитывают поправку лага на данном пробеге для заданного числа оборотов. Коэффициент лага рассчитывается или непосредственно из результатов наблюдений
кл = S / (ол2 — ол1)
или через найденную поправку лага
кл = 1 + Δ л / 100 (47)
Для получения поправок и коэффициентов лага, соответствующих средним скоростям хода корабля, полученным из двух, трех и четырех пробегов на мерной линии, они рассчитываются по следующим формулам:
при двух пробегах —
Δ лср = {Δ л1 + Δ л2) / 2
клср = (кл1 + кл2) / 2 ;
при трех пробегах -
Δ лср = (Δ л1 + 2Δ л2 + Δ л3) / 4;
клср = (кл1 + 2кл2 + кл3) / 4;
при четырех пробегах —
Δ лср = {Δ л1 + 3 Δ л2 + 3 Δ л3 + Δ л4} / 8 ;
клср = { кл1 + 3кл2 + 3 кл3 + кл4} / 8,
где Δ лi — поправка лага, полученная из наблюдений и вычислений на i - м пробеге.
Другой, более точный способ определения поправки и коэффициента лага основан на наблюдениях и
последующем сравнении скорости Vлi полученной по показаниям лага без учета его поправки, со средней скоростью V0, полученной из наблюдений на данном режиме работы движителей.
Для повышения точности и надежности результатов в этом способе на каждом пробеге производится не менее чем три наблюдения скорости V'лi, из результатов которых затем вычисляется Vлi, как их среднее арифметическое.
Каждое наблюдение состоит в том, что по счетчику пройденного расстояния замечаются два отсчета ол1, ол2 и два соответствующих им отсчета моментов времени T1, T2. Затем рассчитываются рол = ол2 - ол1 и время t = Т2 - Т1, выраженное в секундах. На основе полученных данных нетрудно рассчитать скорость корабля V'лi, отнесенную к единице времени — часу:
V'лi = (ролi / ti) * 3600.
Осредненные затем результаты V'лi дают возможность получить среднюю скорость на пробеге Vлi, которая и служит вместе со средней скоростью V0 для непосредственного вычисления поправки и коэффициента лага:
Δ лi = {(V0 - Vлi) / Vлi} * 100 (48)
клi = V0 / Vлi (49)
Полученные таким образом на каждом пробеге поправки и коэффициенты лага осредняются (как и в первом способе) с целью получения средних (Δлср, клср) их значений для каждого режима работы движителей.
По результатам определения поправок лага вычерчивается график, аналогичный графику скоростей хода. По оси абсцисс откладываются скорости хода корабля, а по оси ординат—поправки лага. Вычерченная по нескольким точкам (рекомендуется из наблюдений получать не меньше пяти точек) кривая дает возможность составить Таблицу поправок лага, которая так же, как и Таблица соответствия скорости хода числу оборотов движителей, помещается в навигационный журнал для использования в счислении пути корабля.
Однако опыт и практика работы корабельных штурманов показывают, что более удобно и с большей точностью можно получить данные о скорости и поправке лага не из таблиц, а из графиков, послуживших основанием для составления этих таблиц. Поэтому мы рекомендуем штурманам пользоваться главным образом графиками.
В случаях когда отсутствует возможность произвести необходимые наблюдения на мерной линии, скорость хода корабля при заданном числе оборотов винтов и соответствующая этой скорости поправка лага могут быть определены непосредственно в походе. Скорость хода при этом определяется по продолжительности плавания корабля прямым курсом между двумя обсервованными точками. Поправка лага определяется также путем сравнения действительно пройденного кораблем расстояния с разностью отсчетов лага, соответствующей этому расстоянию.
Если точно определить два места корабля, между которыми рассчитываются скорость хода и поправка лага, не представляется возможным, можно воспользоваться следующим приемом. Курс корабля прокладывается параллельно прямой, соединяющей два маяка или два иных навигационных ориентира. Измерив время плавания этим курсом между траверзами на избранные ориентиры и заметив в моменты траверзов отсчеты лага, можно рассчитать скорость хода и поправку лага, пользуясь формулами (42) и (46). Моменты выхода корабля на траверзы ориентиров следует замечать не по азимутальному кругу, а с помощью картушки компаса по рассчитанному компасному пеленгу.
Штурман должен знать, что последний способ определения поправки и коэффициента лага является весьма приближенным и обращаться к нему следует лишь при острой необходимости, когда, например, нет уверенности в исправности или поправке лага.
Следует иметь в виду, что скорости хода и поправки лага, определенные по расстоянию между двумя обсервованными точками или траверзами на два ориентира, могут содержать значительные ошибки, вызванные неучтенным влиянием течения, ветра, волны и других факторов. В ,таких случаях по результатам наблюдений вычисляется скорость хода не относительно воды, как это имеет место на мерной линии по 2, 3 и 4 пробегам, а действительная скорость перемещения корабля относительно дна моря, соответствующая не только заданному режиму движения, но и конкретным метеорологическим и гидрологическим условиям плавания данным курсом в данном районе моря. Вместо поправки лага в таких случаях определяется так называемая поправка плавания. Полученные таким способом поправка плавания и скорость корабля пригодны для расчета пройденных кораблем расстояний лишь в таких же условиях, в каких они определялись и для грубого контроля за работой лагов.
Глава 4
ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ КАРТОГРАФИЧЕСКИХ ПРОЕКЦИИ
§ 19. Понятие о картографической проекции. Карта. План
Понятие о картографической проекции. Как известно, положение любой точки на поверхности Земли определяется ее географическими координатами—широтой (φ) и долготой (λ). В более общем случае положение точки на земной поверхности может быть определено и в других системах координат — горизонтной, полярной, прямоугольной и т. д.
Положение точки на карте, являющейся изображением сферической (сфероидической) поверхности Земли, также должно определяться пересечением двух координатных линий, которые однозначно соответствовали бы координатным линиям на земной поверхности. Иначе говоря, при изображении сферической поверхности на плоскости необходимо, чтобы каждой точке на поверхности сферы однозначно соответствовала бы точка плоскости, являющаяся ее изображением. При этом непрерывной линии перемещения некоторой точки A0 на сфере должна соответствовать непрерывная линия перемещения ее изображения (точки А) на плоскости карты.
Способ условного изображения поверхности сферы (эллипсоида) на плоскости называют картографической проекцией. В более узлом смысле картографическая проекция — это способ условного изображения на плоскости координатной сетки, соответствующей координатным линиям шара или эллипсоида. Таким образом, сущность всякой картографической проекции состоит в том, что положение любой точки сферической поверхности с координатами φ и λ определяется на плоскости карты картографическими координатами x и y:
x = f1(φ , λ)
y = f2 (φ , λ)
Значения функций f1и f2 находятся, исходя из поставленных условий. Например, вывод уравнений проекции Меркатора производится для условия равноугольности (отсутствие искажений углов) и изображения локсодромии (линии курса) прямой линией.
Карта.
Географической картой называется уменьшенное обобщенное изображение земной поверхности на плоскости, полученное по определенному математическому закону и передающее размещение, состояние и взаимосвязь различных явлений природы и общества. В частности, морские навигационные карты изображают рельеф морского дна, прибрежных участков суши и островов, их взаимное расположение, содержат необходимые для мореплавателя сведения по магнитному склонению, течениям, навигационному оборудованию театра и т. д.
Земля, имеющая в действительности форму геоида, для практических целей кораблевождения принимается за шар или эллипсоид вращения, близкий к геоиду. Эллипсоидальную или сферическую поверхность при картографировании невозможно развернуть в плоскость без складок или разрывов, поэтому переход от шара (эллипсоида) к плоскости осуществляется при помощи математически обоснованных проекций. При этом для избежания разрывов и складок изображение Земли по определенным направлениям искусственно, но закономерно растягивается или сжимается, в результате чего карта не дает полного подобия местности.
План.
При изображении на плоскости небольшого участка земной поверхности ее кривизной можно пренебречь, если возникающие за счет этого погрешности лежат в пределах точности графических построений (0,2 мм на карте). В этом случае все линии изображаемого участка измеряются непосредственно на местности, длины всех линий уменьшаются в одно и то же число раз и наносятся без каких-либо поправок на топографический планшет или бумагу. Такой чертеж носит название плана и характеризуется тем, что искажения углов и длин практически отсутствуют, а степень уменьшения изображения (масштаб) одинакова во всех его точках и по всем направлениям. По сравнению с планом карта представляет собой изображение более обширных участков земной поверхности на плоскости, при котором возникающие искажения могут превышать точность графических построений. Поэтому перенос, или проектирование, земной поверхности на плоскость карты производится с учетом переменного масштаба в разных ее частях, обусловленного математическим законом данной проекции.


§ 20. Нормальная, поперечная и косая картографические сетки
Система сферических координат, которая проще всего изображается на плоскости в данной проекции, называется нормальной системой сферических координат.
Нормальной, картографической сеткой называется изображение на плоскости нормальной системы сферических координат. Нормальную сетку часто называют прямой.
Поперечной картографической сеткой называется изображение на плоскости системы географических координат (меридианов и параллелей), когда географический полюс (точка Ро на рисунке б ) повернут на 90° от направления на полюс (Zо )нормальной системы сферических координат.
Косой картографической сеткой называется изображение на плоскости в данной проекции системы географических координат, когда географический полюс (точка Ро на рисунке а) повернут от направления на полюс (Zо) нормальной системы сферических координат на угол, не равный 0 и 90°.

Для большинства проекций нормальной системой координат на сфере является горизонтная система с координатными линиями вертикалов и альмукантаратов; полюсом такой сетки является точка зенита Zо.
Если точка Zо совпадает с полюсом Земли (рисунок а), то нормальная система совпадает с географической (основной), которая будет изображена на плоскости данной проекции в виде нормальной сетки координат.
В этом случае географическая система координат называется нормальной, а картографическая проекция — прямой.
Применение нормальной, поперечной и косой сеток зависит от географического положения картографируемого участка земной поверхности. Так, для изображения экваториальных стран обычно строится нормальная сетка географических меридианов и параллелей, для полярной области—поперечная, для средних широт — косая сетка.
При построении поперечных и косых сеток первоначально по формулам сферической тригонометрии производится пересчет координат узловых точек пересечения наносимых меридианов и параллелей из географической системы в нормальную. Затем по формулам данной проекции рассчитываются картографические координаты узловых точек, по которым и строится основная сетка географических меридианов и параллелей.

 § 21. Масштаб карты. Характеристика искажений проекции
§ 21. Масштаб карты. Характеристика искажений проекции
Чтобы изобразить тот или иной участок земной поверхности на карте или плане, необходимо предварительно уменьшить его размеры. Для удобства введено понятие условный глобус, т. е. глобус, подобный земному эллипсоиду, степень уменьшения которого называется общим или главным масштабом карты. Карта же изображает земную поверхность или часть ее с условного глобуса в масштабе 1:1.
В отличие от частного главный масштаб характеризует общее уменьшение изображения на карте, он задается при вычислении картографической сетки в заданной проекции и подписывается на карте. Главный масштаб сохраняет свое численное значение лишь в определенных точках карты или вдоль некоторых определенных направлений (линий) в зависимости от характера проекции. Точка карты или направление (линия), в которых масштаб изображения равен главному масштабу, называется центральной точкой или центральной линией проекции.
Как уже упоминалось, проектирование эллипсоидальной (или сферической) поверхности глобуса на плоскость проекции — карту — не может быть осуществлено без разрывов или складок. Для заполнения таких складок и разрывов земная поверхность условного глобуса изображается на карте не в одинаковом масштабе, а с некоторыми искажениями, выраженными определенными математическими законами и, следовательно, поддающимися строгому учету. Эти законы выражаются уравнениями проекции. Например, если поверхность Земли на условном глобусе разрезать на небольшие меридиональные доли и затем перенести их на плоскость, то получатся разрывы изображения, увеличивающиеся по мере удаления от экватора, т. е. с увеличением широты (рисунок).
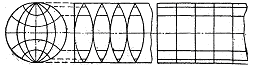
Растянув дольки по параллелям, получим карту Земли в квадратной проекции. Меридианы на этой проекции сохраняют свою длину соответственно главному масштабу, а параллели растягиваются до длины окружности экватора условного глобуса. Следовательно, искажений по направлению меридианов не будет, искажения по направлениям параллелей будут наибольшими и при этом увеличиваются от экватора к полюсам пропорционально косинусу широты. При других видах проекций характер искажений будет иным, но наличие искажений неизбежно. При этом искажения равны нулю около центральных точек или линий проекции, возникая и увеличиваясь по мере удаления от них.
Вследствие наличия искажений в картографии различают главный масштаб (µ о) и частный масштаб (µ) определяемые следующими формулами:
µ o = dso / dSo (50)
µ = ds / dSo (51)
где dso — бесконечно малый отрезок на условном глобусе;
dSo — соответствующий ему отрезок на поверхности Земли (в натуре);
ds — бесконечно малый отрезок на карте.
Таким образом, масштабом в данной точке карты называется отношение бесконечно малого отрезка (ds), взятого около данной точки по данному направлению, к горизонтальной проекции соответствующего ему отрезка на местности (dSо).
Главный масштаб характеризует общее уменьшение изображения, а частный масштаб характеризует степень уменьшения только в данной точке карты. Отношение частного масштаба в данной точке по данному направлению к главному масштабу называется увеличением масштаба и характеризует степень искажения проекции или масштаб карты по отношению к условному глобусу:
c = µ / µo = (ds : dSo) / (dso : dSo) = ds / dso (52)
В общем случае увеличение масштаба меняется при переходе от одной точки проекции к другой, а также по разным направлениям около одной и той же точки. Это приводит к искажению длин, направлений, углов и площадей на проекции.
Увеличение масштаба характеризует изменение частного масштаба и представляет собой множитель, на который нужно умножить главный масштаб, чтобы получить частный µ = cµo. Чем ближе увеличение масштаба с к единице во всех точках карты, тем, следовательно, лучше и совершеннее выбранная для данной карты проекция.
Разность между увеличением масштаба с и единицей называется относительным искажением длин или просто искажением длин:
v = c - 1
v = µ / µо - 1 = (µ - µo) / µo (53)
При известных главном масштабе карты и частном масштабе по заданному направлению искажение длин в данной точке карты может, быть подсчитано сравнительно просто. Например, если главный масштаб µо =1 : 500 000, а частный масштаб µ =1 :434 780, то увеличение масштаба
с = µ / µo = 1,15, искажение длин v = c - 1 = 0,15 = +15%.
Пусть на карте отрезок равен 50 мм, что в главном масштабе 1:500000 соответствует расстоянию в 25 000 м. Следовательно, действительное расстояние на местности, соответствующее данному отрезку карты, будет равно 25000: 1,15=21739 м.
Обобщенная характеристика искажений проекций производится с помощью эллипса искажений, который здесь пока не рассматривается.
На картах масштаб выражается в двух видах: численном и линейном.
Численным или числовым масштабом называется отношение данной линии на условном глобусе к длине соответствующей ей линии на местности. Числовой масштаб изображается в виде дроби: 1/50000; 1/750000 и т. д.;
знаменатель показывает, какова степень уменьшения длин на условном глобусе.
Числовой масштаб может быть задан и в таком виде: 1:100000; 1:250000; 0,000001; 0,00004 и т. д.
При графической работе на карте применяется линейный масштаб, показывающий число единиц, принятых для измерения длин на местности (км, мили), содержащихся в единице, принятой для измерения длин на карте (мм, см). Например, линейный масштаб на специально вычерченной шкале показывает число километров, содержащихся в одном миллиметре, число миль в одном сантиметре и т. п.
На морских навигационных картах в проекции Меркатора линейный масштаб разбивается вдоль боковых рамок карты. На топографических картах (и географических) линейный масштаб чертится под нижней рамкой карты в виде короткой шкалы.
С уменьшением масштаба карты изображения небольших объектов становятся настолько малыми, что нанесение их на карту становится невозможным. Практикой установлено, что невооруженный глаз человека способен различать на бумаге расстояния, если они не меньше 0,1 мм. Две точки, находящиеся на расстоянии менее 0,1 мм одна от другой, будут казаться слившимися в одну. В соответствии с этим свойством глаза человека принято линейное расстояние на местности, соответствующее на карте отрезку в 0,1 мм, называть предельной точностью масштаба. Однако при составлении карты неизбежны некоторые неточно-сти за счет ошибок при вычерчивании контуров, ошибок фотографирования и ошибок за счет деформации бумаги. Поэтому при работе на карте условились за предельную точность масштаба принимать расстояние на местности, соответствующее отрезку карты, равному 0,2 мм.
Предельная точность масштаба зависит от масштаба карты и рассчитывается следующим образом. Пусть дан масштаб 1 :500 000, т. е. 1 мм карты соответствует отрезок на местности, равный 500000 мм, а следовательно, 0,2 мм карты будет соответствовать отрезок на местности, равный 100 м. Таким образом, предельная точность масштаба 1:500000 равна 100 м.
Масштаб и предельная точность масштаба определяют количество подробностей, наносимых на карту, и ту точность, с которой на карте могут выполняться графические построения.


§ 23. Классификация картографических проекций
Картографические проекции можно классифицировать по различным признакам. Однако с точки зрения построения и практического использования карт наиболее употребительными признаками их классификации служат:
—характер искажений проекций, обусловливающий возможности практического использования карт;
— вид меридианов и параллелей нормальной сетки.
По характеру искажений все картографические проекции делятся на четыре группы:
— равноугольные, или конформные;
— равновеликие, или эквивалентные (равноплощадные);
— равнопромежуточные (эквидистантные);
— произвольные.
Равноугольные проекции. Основным свойством равноугольных, или конформных, проекций является сохранение подобия малых фигур на карте соответствующим фигурам на поверхности Земли. Равноугольные проекции не искажают углов. Бесконечно малый круг на такой проекции изображается также кругом. Однако при сохранении неискаженными углов и направлений в равноугольной проекции искажаются линейные размеры и площади фигур. Масштаб в таких проекциях зависит от направления. Эллипсы искажений, обращаясь во всех точках карты в окружности, имеют размеры, зависящие от положения точки.
Условие равноугольности картографической проекции можно записать следующим образом:
a = b; m = n.
Постоянство частного масштаба в данной точке по всем направлениям облегчает производство измерений на карте, составленной в равноугольной проекции. Для учета изменения масштаба при измерении больших отрезков их следует измерять на карте по частям.
Свойство конформности позволяет на картах, составленных в таких проекциях, измерять углы и азимуты непосредственно с помощью транспортира. Эти свойства обусловили широкое применение равноугольных проекций для построения морских карт. Отметим, что равноугольные проекции сохраняют равными углы, но не кривизну линий, поэтому подобие сохраняется только для малых фигур.
К равноугольным проекциям относятся проекции Меркатора, Гаусса, стереографическая и некоторые другие.
Равновеликие проекции. Равновеликие, или эквивалентные, проекции не обладают свойством подобия фигур, но сохраняют масштаб площадей в пределах всей карты одинаковым. Это означает, что равным между собой площадям на местности соответствуют равные между собой площади на карте. Бесконечно малый кружок на местности изобразится на карте в равновеликой проекции эллипсом, площадь которого равна площади кружка на глобусе. Любая замкнутая фигура произвольных размеров на глобусе изобразится на проекции не подобной, но равновеликой ей замкнутой фигурой. Формы эллипсов искажений в разных точках карты будут различными, площади же их обязательно будут равны площадям соответствующих кружков на глобусе.
Математическое условие равновеликости можно записать следующим образом:
Дата добавления: 2014-12-22; просмотров: 1950;
