Комплексный (символический) метод расчета цепей синусоидального тока
Вектор синусоидально изменяющейся величины может быть представлен и на комплексной плоскости. Комплексные представления позволяют совместить простоту и наглядность векторных диаграмм, имеющим недостаток – ограниченную точность, с возможностью проведения точных аналитических расчетов. При оперировании с векторами можно воспользоваться теорией, разработанной для комплексных чисел. Вектору, расположенному на комплексной плоскости, однозначно соответствует комплексное число. В соответствии с формулой Эйлера для комплексного числа равнозначны алгебраическая, тригонометрическая и показательная формы записи. При суммировании комплексных чисел удобна алгебраическая форма, при умножении и делении – показательная.
Использование комплексной формы представления позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. В результате этого к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока.
Следует обратить внимание на то, что комплексные изображения, как и векторные диаграммы, несут информацию только о двух параметрах синусоиды – амплитуде и начальной фазе, не отражая ее третьего параметра – угловую частоту ω. Векторы на комплексной плоскости и соответствующие им комплексные числа принято изображать той же буквой, что и амплитуду изображаемой синусоиды с точкой наверху.
Мнимая единица в электротехнике обозначается символом j , поскольку символ i используется для обозначения мгновенного тока.
Ток i(t) = Im sin(ωt + φо) можно представить комплексным числом Ím на комплексной плоскости
где амплитуда тока Im – модуль, а угол φо, являющийся начальной фазой, – аргумент комплексного тока.
Все параметры цепи представляются в комплексной форме.
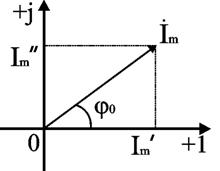
Алгебраическая форма записи комплексного числа: İm = Im’ + j Im’’, при записи в тригонометрической форме проекции вектора выражают через его длину Im и угол φо: İm = Imcosφо + j Imsinφо = Im(cosφо + j sinφо). Показательная форма записи имеет вид İm = Ime jφо .
В этих выражениях Im = √ (Im’ 2+ Im’’2 ) – модуль комплексного числа, φо = arctg(Im’’/ Im’) - его аргумент, Im’= Imcos φо, Im’’= Imsin φо.
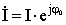 – комплексное действующее значение силы тока (без индекса m); здесь I = Im/√2;
– комплексное действующее значение силы тока (без индекса m); здесь I = Im/√2;
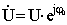 – комплексное действующее значение напряжения (без индекса m); U =Um/√2.
– комплексное действующее значение напряжения (без индекса m); U =Um/√2.
Пример, представить комплексное действующее значение тока 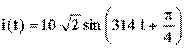
в показательной форме. Ответ:
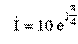 .
.
Дата добавления: 2014-12-22; просмотров: 1431;
