Переменный ток в цепи с последовательным соединением элементов R, L, C
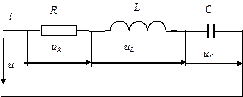
|
Предположим, что имеется цепь, содержащая резистор R, катушку с индуктивностью L и конденсатор с емкостью С. Подведем к зажимам цепи переменное напряжение u. По цепи потечет переменный ток i. На отдельных участках цепи возникнут падения напряжений, для которых в соответствии со вторым законом Кирхгофа можно записать:
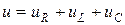 .
.
Определим, какую форму изменения будут иметь падения напряжений на участках цепи, если ток изменяется по закону:
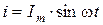 .
.
Падения напряжений на участках цепи определяются из соотношений известных из курса физики:
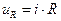 ,
, 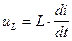 ,
, 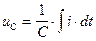 ( i=C
( i=C 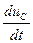 ).
).
После подстановки в исходные уравнения значения тока i получим:
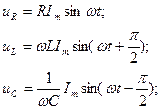 (т.к. (sin kx)’ = k cos kx, = k sin(kx+π/2 ))
(т.к. (sin kx)’ = k cos kx, = k sin(kx+π/2 ))
( т.к. ∫ sin kx dx = - 1/k cos kx).
Проанализируем полученные уравнения. Величины 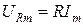 ,
, 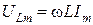 и
и 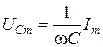 имеют размерность [B] и представляют собой соответственно амплитудные значения напряжений резисторе, катушке индуктивности и конденсаторе.
имеют размерность [B] и представляют собой соответственно амплитудные значения напряжений резисторе, катушке индуктивности и конденсаторе.
Величины R, 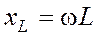 и
и 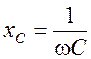 имеют размерность [Ом] и называются соответственно: R - активное сопротивление, xL - реактивное индуктивное сопротивление, xC - реактивное емкостное сопротивление.
имеют размерность [Ом] и называются соответственно: R - активное сопротивление, xL - реактивное индуктивное сопротивление, xC - реактивное емкостное сопротивление.
Активное сопротивление R не зависит от частоты тока, а реактивные сопротивления xL и xC являются функцией частоты тока 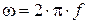 .
.
Сравнение фаз тока и напряжений позволяет сделать следующие выводы:
− в цепи с активным сопротивлением ток и напряжение совпадают по фазе j=0;
− в цепи с индуктивностью ток отстает от напряжения на угол 90°;
− в цепи с емкостью ток опережает напряжение на 90°.
Для соответствующих участков электрической цепи векторные диаграммы токов и напряжений будут выглядеть следующим образом.
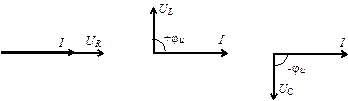
|
Дата добавления: 2014-12-22; просмотров: 1279;
