Операция импликации, или импликация высказываний

Высказывание С, составленное из высказываний А и В при помощи слов «если…, то…», называют импликацией высказываний А и В и 1б1-начают

(выражение 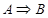читается «из А следует В», или «если А, то В»).

Импликация ложна только в том случае, когда А – истинное высказывание, а В – ложное. Во всех других случаях импликация имеет значение «истина».

Таблица истинности для операции импликации:

А	В

Первый член импликации 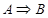, – высказывание А, – называется посылкой, или условием, а второй член В – заключением.

Обратите внимание, что таблица истинности для импликации, в отличии от таблиц для конъюнкции, дизъюнкции и эквивалентности, изменяется при перестановке столбцов для А и В.

Отметим также, что импликация не полностью соответствует обычному пониманию слов «если…, то…» и «следует». Из третьей и четвёртой строк таблицы истинности для импликации вытекает, что если А – ложно, то, каково бы ни было В, высказывание 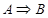считается истинным. Таким образом, из неверного утверждения следует всё что угодно.

Например, утверждения «если 6 – простое число, то 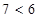» или «если 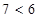, то существуют ведьмы» являются истинными. Истинным является и рассмотренное ранее высказывание: «если слон – насекомое, то Антарктида покрыта тропическими лесами».

Для иллюстрации содержательного смысла импликации рассмотрим ещё один пример.

Пусть 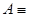{папа завтра получит премию},

{папа завтра купит сыну велосипед}.

Импликация 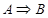может быть сформулирована так:

«если папа завтра получит премию, то купит сыну велосипед».

Пусть А и В – истинны. Тогда папа, получив премию, покупает сыну велосипед. Естественно считать это истинным высказыванием.

Если же папа, получив премию (А – истинно), не купит сыну велосипед (В – ложно), то это, можно сказать, – не логичный поступок, и импликация имеет значение «ложь».

Если папа не получит премию (А – ложно), но купит велосипед (В – истинно), то результат положителен (импликация истинна).

Наконец, в том случае, если, не получив премии (А – ложно), папа не купит велосипед (В – ложно), то обещание не нарушено, импликация истинна.

Задача 1. Даны два высказывания 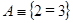и . В чём заключаются высказывания , , 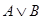, 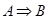? Какие из этих высказываний истинны и какие ложны?

Решение.

1) Высказывание , очевидно, ложно. Для того чтобы произведение двух высказываний было истинным, нужно чтобы оба высказывания были истинными.

2) Высказывание 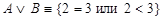истинно, т.к. одно из слагаемых является истинным высказыванием.

Высказывание 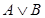можно записать в виде одного верного нестрогого неравенства .

3) Эквивалентность ( тогда и только тогда, когда 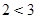) представляет собой ложное высказывание, т.к. А – ложно, а В – истинно.

4) Импликация 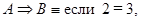то 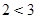является истинным высказыванием.

В самом деле, импликация 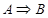согласно определению ложна только тогда, когда А – истинно, а В – ложно.