Поправка в вольтах равна

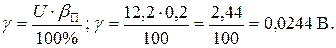
Погрешность этой поправки равна погрешности измерения 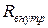, т.е.

Исправленное значение поправки с учетом округления будет равно:

Исправленное показание вольтметра будет равно (с учетом округления)

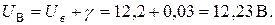
Определим суммарную систематическую погрешность исправленного результата измерений.

Основная погрешность, определяемая классом точности прибора

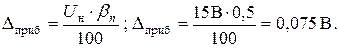
Дополнительная погрешность, обусловленная температурным отклонение от нормальной

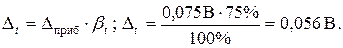
Дополнительная погрешность, обусловленная воздействием магнитного поля

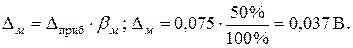
Суммарная систематическая погрешность 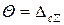, вероятностью Р = 0,95 вычисляется по формуле

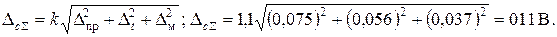
Результат измерения запишется в виде

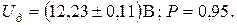
161. Определить методическую погрешность измерения мощности, обусловленную потреблением энергии измерительными приборами. Показание амперметра 0,75 А, вольтметра – 150 В. Сопротивление амперметра 0,5 Ом, сопротивление вольтметра 10000 Ом. Классы точности: амперметра 1, вольтметра 0,5. Номинальные значения приборов I_н = 1 А и U_н = 250 В. Определите погрешность измерения мощности, обусловленную неточностью приборов.

Решение:

При измерении мощности, потребляемой нагрузкой R_н, можно использовать две схемы включения (см. рис. 48 и 49)

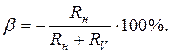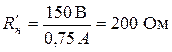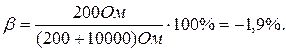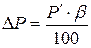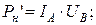
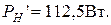
При схеме включения рис. 49 относительная методическая погрешность равна Вычисленное сопротивление, нагрузки по показаниям приборов равно . Тогда погрешность, обусловленная потреблением энергии вольтметром будет равна Поправка (берется с отрицательным знаком) к результату измерения будет равна , 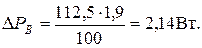Значение мощности потребляемой нагрузкой будет равно , где Р_н’ – мощность, вычисления по показаниям приборов.

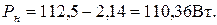
При использовании схемы рис. 48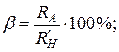

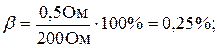
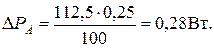
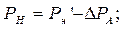
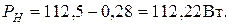
Т.к. во втором случае вносимая погрешность меньше, примем за результат значение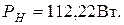

Поскольку мощность определяется методом амперметра и вольтметра, т.е. косвенно, то для вычисления инструментальной погрешности, обусловленной неточностью приборов, воспользуемся соответствующими формулами:

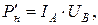
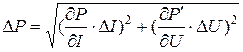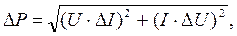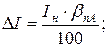
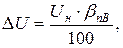
; где 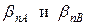- относительные приведенные погрешности, соответствующие классам точности приборов.

; ;

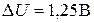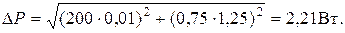
Искомый результат однократного измерения мощности будет равен

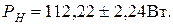
162. Сопротивление резистора R_x определяется с помощью амперметра и вольтметра. Показание амперметра класса точности 0,5 и номинального значения 2,5 А равно 2 А, показание вольтметра класса точности 0,2 и номинального значения 300 В равно 200 В. Сопротивление вольтметра 5000Ом, сопротивление амперметра 0,4 Ом. Определить методическую абсолютную и относительную погрешность измерения при различных схемах включения измерительных приборов (рис. 48, 49). Ввести поправку в результат. Вычислить окончательный результат измерения с учетом классов точности приборов.

163. Мощность, выделяющаяся на резисторе R_H, сопротивление которого известно и равно 100±5 Ом, определяется с помощью вольтметра, присоединенного параллельно этому резистору. Показание вольтметра равно 50 В. Вольтметр имеет класс точности (1) и собственное сопротивление 3·10⁴ Ом. Определить методическую относительную и абсолютную погрешности измерения. Внести поправку в результат и определить окончательный результат значения мощности с учетом класса точности вольтметра.

164. Напряжение источника ЭДС U_х с внутренним сопротивлением R_i = 8±0,5 Ом. Измеряют вольтметром класса точности 0,5 с собственным сопротивлением R_В =10 кОм. Показание вольтметра U_В = 11,65 В. Найти поправку, которую нужно внести в показание прибора. Вычислить действительное значение напряжения источника ЭДС с учетом класса точности вольтметра, если номинальное значение вольтметра равно U_н = 15 В.

165. Определить погрешность результата однократного измерения напряжения U = 15 В на сопротивлении 150 Ом, выполненного вольтметром на номинальное значение U_н = 30 В и классом точности 1,5. Внутреннее сопротивление вольтметра R_В = 3 кОм. Дополнительные погрешности из-за наличия магнитного поля и повышенной температуры в процессе измерения составляет соответственно 50% и 75% от основной погрешности вольтметра. Определить доверительный интервал результата при Р = 0,9 (k = 0,95).

166. Вольтметром с номинальным значением 75В и классом точности (1) измеряется напряжение на резисторе 35 Ом. Показание вольтметра 70 В. Дополнительные погрешности из-за влияния магнитного поля и повышенной температуры равны соответственно 0,3 и 0,2 части от основной погрешности, определяемой классом точности прибора. Определите погрешность результата однократного измерения. Определите погрешность результата однократного измерения при доверительной вероятности Р = 0,9 (k = 0,95).

167. Мостом постоянного тока Р349 проводились прямые измерения сопротивления резисторов. Измерения проводились в нормальных условиях. Класс точности моста 0,01.

Были получены следующие результаты: 100,46; 100,36; 100,37; 100,50; 100,49; 100,38; 100,43; 100,39; 100,35; 100,42; 100,47; 100,44; 100,40; 100,47; 100,42 Ом.

Для устранения влияния соединений и контактов был проведен ряд измерений образцового сопротивления с номинальным значением 10 Ом (класса точности 0,001). Были получены результаты: 10,38; 10,43; 10,49; 10,39; 10,35; 10,41; 10,42; 10,44; 10,37; 10,36; 10,45; 10,40; 10,38; 10,39; 10,42Ом.

Требуется провести обработку результатов измерений. Найти результат измерения сопротивлений, доверительный интервал при доверительной вероятности Р = 0,95.

168. Цифровым вольтметром класса 0,5/0,2 проводились многократные измерения падения напряжения на резисторе 60 Ом на пределе 100 В. Были получены результаты 12 измерений: 70,23; 70,19; 70,22; 70,25; 70,21; 70,18; 70,24; 70,17; 70,26; 70,20; 70,25; 70,18В. Входное сопротивление вольтметра 1 МОм. Требуется провести обработку результатов измерений. Найти погрешность измерения напряжения при доверительной вероятности Р = 0,9.

169. Выполнено однократное измерение напряжения U_х на участке электрической цепи сопротивления 25 Ом. Для измерения напряжения использовался вольтметр класса точности 0,5 с номинальным значением 15 В. Условия измерения отличались от нормальных. Показание вольтметра U_В = 9 В, сопротивление вольтметра R_В = 1000 Ом. По паспортным данным было установление, что дополнительная температурная погрешность составляет 0,4 от основной погрешности, а погрешность от влияния магнитного поля 0,5 от основной погрешности. Определить суммарную погрешность измерения и записать результат в стандартной форме. Принять доверительную вероятность Р = 0,9 (k = 0,95).

170. Амперметром измерялся ток в цепи. Класс точности амперметра 1, его номинальное значение 0,5 А, собственное сопротивление R_A = 0,1Ом. Сопротивление цепи R_ц = 10 Ом, показание амперметра 0,453 А. Условия измерения были отличны от нормальных. Дополнительные погрешности от влияния температуры и магнитного поля составили по 0,5 части от значения основной погрешности амперметра. Определить суммарную абсолютную и относительную погрешности. Записать результат в стандартной форме. При решении задачи учесть, что систематическая погрешность, обусловленная сопротивлением амперметра, отличным от нуля рассчитывается по формуле 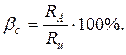Принять доверительную вероятность Р = 0,9 (k = 0,95).

171. Цифровым вольтметром класса точности 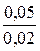на пределе измерения 10 В получено одиннадцать измерений падения напряжения на резисторе R = 100 Ом. Сопротивление вольтметра 0,5 МОм. Получен ряд наблюдения: 7,482; 7,480; 7,478; 7,450; 7,486; 7,490; 7,484; 7,320; 7,476; 7,488; 7,475 В. Распределение результатов считать нормальным. Выяснить, нет ли в ряду измерений промахов. Определить результат измерения и доверительный интервал при доверительной вероятности 0,95.

172. Цифровым вольтметром класса точности 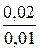на пределе измерения 100 В произведено одиннадцать измерений падения напряжения на резисторе сопротивлением (1000±50) Ом. Сопротивление вольтметра 0,5 МОм. Получен ряд наблюдения: 92,64; 92,50; 92,70; 92,65; 92,67; 90,31; 92,67; 92,37; 92,43; 92,68; 92,73; 92,68 В.

Распределение результатов подчиняется нормальному распределению. Выяснить, нет ли в ряду наблюдений промахов. Определить результат измерения и доверительный интервал при доверительной вероятности Р = 0,98.

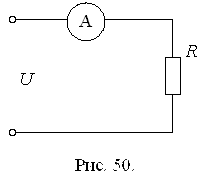
173. Амперметром магнитоэлектрической системы с номинальным значением 5 А, класса точности 0,2 и собственным сопротивлением 0,5 Ом измеряется ток в цепи по схеме, приведенной на рис. 50. Сопротивление резистора R = 5±0,5 Ом. Измерения проводятся при температуре 30⁰С. В паспортных данных для амперметра указано, что температурная погрешность прибора составляет 50% от основной погрешности на каждые 10⁰С отклонения от нормальной температуры. Получен ряд наблюдений: 3,91; 3,93; 3,92; 3,95; 3,90; 3,89; 3,98; 3,53; 3,87; 3,96 А. Распределение результатов подчиняется распределению Стьюдента. Выяснить, нет ли в ряду наблюдений промахов. Определить результат измерения и доверительный интервал при доверительной вероятности Р = 0,95.

174. Активная энергия в цепи переменного тока измерялась косвенным методом с помощью амперметра, вольтметра, фазометра и хронометра. Номинальное значение амперметра 5 А, класс точности 1; номинальное значение вольтметра 250 В, класс точности 0,5. Погрешность хронометра ±10 сек в сутки. Класс точности фазометра 2,5. Измерение энергии производилось в течение 30 сек. Показание амперметра 4 А, показание вольтметра 220 В, показание фазометра 0,9. Определить результат измерения и доверительный интервал результата при доверительной вероятности Р = 0,9.

175. Электромагнитным вольтметром класса точности 0,5 и номинальным значением 30 В измерялось падение напряжения на резисторе 300 Ом. Сопротивление вольтметра 10 кОм. Измерения проводились при температуре 30⁰С и влиянии магнитного поля напряженностью Н = 400 А/м. Из паспортных данных вольтметра известно, что температурная погрешность вольтметра равна 25% от основной, а магнитная погрешность 0,75% от основной погрешности. Получен ряд наблюдений: 25,37; 25,21; 25,39; 24,43; 25,32; 25,44; 25,49; 24,23 В. Распределение результатов подчиняется распределению Стьюдента. Выяснить, нет ли в ряду наблюдений промахов. Определить результат измерения и доверительный интервал при доверительной вероятности Р = 0,9.

Решение:

а) Находим среднее арифметическое результатов:

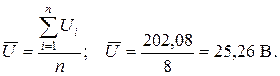
б) Определим остаточные суммы :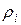

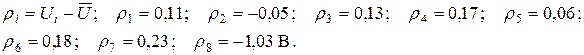
в) Определим сумму остаточных сумм: 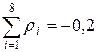В. Это довольно большая величина, свидетельствующая о возможности промаха. Подозрительным является результат 24,23 В.

г) Найдем сумму квадратов остаточных сумм .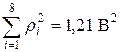

д) Определим оценку среднего квадратического отклонения среднего арифметического ряда наблюдений:

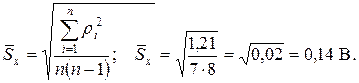
е) Для анализа ряда измерений на наличие промаха воспользуемся статистическим критерием:

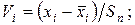
если 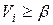, то результат 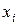является промахом.