Методика конечно-элементного моделирования объемной задачи НДС при пластической деформации

В данном разделе диссертации необходимо определить динамически изменяющееся НДС при прокатке листового металла. Для расчета НДС использовали следующие десять функций [79,80]:

σ_ij = σ_ij (x, y, z, t);

x = x (x₀, y₀, z₀, t);

y = y (x₀, y0, z₀, t); (3.1)

z = z (x₀, y₀, z₀, t);

ρ = ρ (x, y, z, t),

где x₀, y₀, z₀, x, y, z – начальные и текущие координаты материальной точки деформируемого тела;

ρ – плотность;

t – время.

Данные величины называют искомыми механическими переменными. Их находят в очаге деформации в любой момент времени t.

Функции (3.1) связаны дифференциальными уравнениями движения и неразрывности [79, с. 203 – 228, 80, с. 77 – 134]:

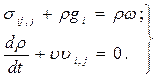(3.2)

В связи с тем, что формулы (3.2) связывают десять неизвестных (шесть для σij, три ωi, а также плотность ρ), их трудно решить математическими методами механики сплошных сред.

Удельные массовые силы g и ускорения ω в большинстве процессов обработки металлов давлением (ОМД) достаточно малы и ими можно пренебречь. Тогда формулы (3.2) преобразуются в дифференциальные уравнения равновесия [49, с. 203 – 228, 80, с. 77 – 134], т.е.

Для решения системы уравнений (3.1) недостает шести уравнений. Данные уравнения в теории прокатки определяют исходя из свойств деформируемого металла. В теории прокатки эти шесть уравнений называют физическим уравнением связи НДС [79, с. 203 – 228, 80, с. 77 – 134].

Из теории прокатки известно [83,84,85], что во многих случаях компоненты девиаторов напряжения и скорости деформации пропорциональны. В теории пластичности такую пропорциональность называют пропорциональностью девиаторов напряжения и скорости деформации.

Используя гипотезу пропорциональности девиаторов напряжения и скорости деформации можно вывести формулу [81,с. 16 – 93, 82, с. 32 - 132, 83, с.13 – 57]:

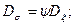
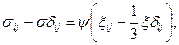(3.3)

где ψ – скалярный множитель.

Величину скалярного множителя ψ можно определить с помощью следующего соотношения [81,с. 16 – 93, 82, с. 32 - 132, 83, с.13 – 57]:

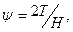(3.4)

где Т – интенсивность касательных напряжения;

Н – интенсивность скоростей деформации сдвига.

На основе вышесказанного можно отметить, что для расчета НДС прокатываемой заготовки необходимо определить [81,с. 16 – 93, 82, с. 32 - 132, 83, с.13 – 57]: в каждой точке очага деформации траекторию движения частицы, показатели деформируемого и напряженного состояния. Шесть компонентов тензора напряжений, тензора деформаций, тензора скорости деформаций и три компонента вектора скорости течения характеризуют НДС деформируемой заготовки.

При решении упругопластической задачи прокатки используют систему уравнений, которые являются следствием законов сохранения массы, импульса и энергии. В декартовой системе координат используемые основные уравнения в тензорной форме имеют следующий вид [79, с. 278 – 340, 80, с. 39 – 71]:

- уравнение неразрывности деформаций:

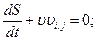(3.5)

- условие постоянства объема:

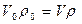; (3.6)

- уравнение движения:

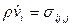; (3.7)

- уравнение теплопроводности:

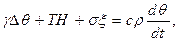(3.8)

где γ – коэффициент теплопроводности;

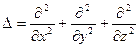– дифференциальный оператор Лапласа;

θ – температура материальной частицы деформируемого тела;

с – удельная массовая теплоемкость;

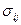- компоненты тензора напряжений;

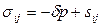, где 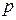определятся как функция .

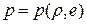Физическими соотношениями в форме Прандтля – Рейса при условии текучести Мизеса можно воспользоваться для описания упруго пластического течения твердого тела [79, с. 278 – 340, 80, с. 39 – 71]:

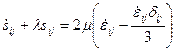, (3.9)

при значении 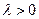деформация пластическая, а при 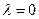- деформация упругая.

В уравнениях (3.5 – 3.9) использованы следующие обозначения [79, с. 278 – 340, 80, с. 39 – 71]: 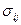, , 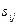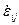– компоненты тензоров напряжения, девиатора напряжений и тензора скоростей деформаций, соответственно; 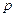– давление; 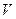– объем; 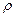– плотность; 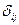– символ Кронекера; каждый из индексов 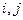последовательно принимает значения 1, 2, 3. Производную по времени обозначает точка над переменной. Производную по соответствующей пространственной переменной обозначает запятая между нижними индексами.

С учетом производной Шаумяна вдоль траектории материальной частицы производится вычисление производной по времени от компонент девиатора тензора напряжений [79, с. 278 – 340, 80, с. 39 – 71]. Поворот элемента тела как жесткого целого относительно исходной системы координат позволяет учесть Шаумяновская производная по времени.

Метод конечных элементов используется для численной реализации решения уравнений (3.5 – 3.9) [84,85,86]. Разбивка деформируемого тела на конечные элементы лежит в основе данного метода. Для объемного моделирования можно использовать геометрическую форму конечного элемента в виде тетраэдра (рисунок 3.4).

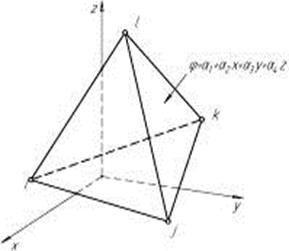
Рисунок 3.4 – Трехмерные конечные элементы

Двенадцать компонент перемещений (по 3 (и_х, и_y, и_z) в каждом узле i, j, k, l) содержит вектор узловых перемещений п-го тетраэдра [86, с. 91 – 152]. Линейным полиномом можно аппроксимировать перемещения j внутри тетраэдра:

,

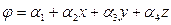где a₁ … a₄ – коэффициенты.

Данные коэффициенты определяются из системы четырех уравнений, т.е. коэффициенты определяются путем подстановки координат узлов и соответствующих им узловых перемещений в уравнении [86, с. 91 – 152]:

.

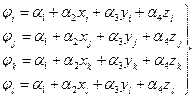Систему уравнений в матричном виде можно записать в следующем виде [86, с. 91 – 152]:

где 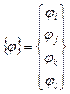- вектор узловых перемещений;

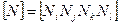- матрица функций формы,

где

,

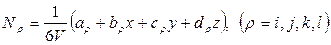через координаты узлов можно определить коэффициенты а_r, b_r, c_r, d_r, т.е.

, , , .

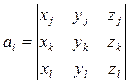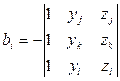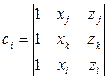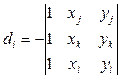Циклической перестановкой индексов можно найти остальные коэффициенты [86, с. 91 – 152]:

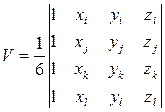- объем тетраэдра i j k l.

Поскольку 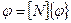, то полный вектор приращений узловых перемещений п-го тетраэдра имеет вид [86, с. 91 – 152]:

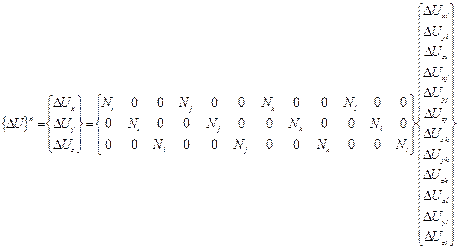. (3.10)

Вектор приращения деформаций п-го тетраэдра имеет вид [86, с. 91 – 152]:

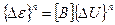. (3.11)

Учитывая N_r и дифференцируя выражения (3.11) по пространственным координатам получена матрица [B] [86, с. 91 – 152], т.е.

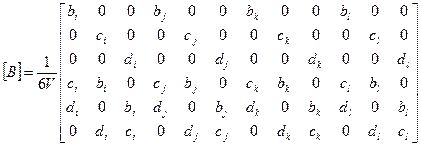. (3.12)

Связаны следующим соотношением приращения напряжений и деформаций п-го элемента [86, с. 91 – 152]:

(3.13)

где [D] и [D_p] – упругая и упругопластическая матрицы «деформации – перемещения» (соответственно написано);

Законом Гука является верхняя формула, пластическое упрочнение отражает нижняя формула [86, с. 91 – 152].

Приращения деформаций и напряжений каждого элемента можно определить через известный полный вектор приращения узловых перемещений [86, с. 91 – 152]. На q-м шаге нагружения текущее значение НДС каждого элемента можно определить по формуле:

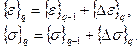(3.14)

Корни кубического уравнения являются главными деформациями ε₁, ε₂, и ε₃ [86, с. 91 – 152]. Для определения компонентов тензора главных деформаций можно воспользоваться выражением [86, с. 91 – 152]:

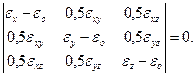(3.15)

Известно, что для главных деформаций выполняется следующее соотношение [86, с. 91 – 152]:

ε₁ ≥ ε₂ ≥ ε₃.

Интенсивность деформаций ε_инт можно рассчитать по формуле [88, с. 91 – 152]:

ε_инт = MAX (|ε₁ − ε₂| · |ε₂ − ε₃| · |ε₃ − ε₁| ). (3.16)

Для определения эквивалентной деформации ε_экв можно использовать формулу [86, с. 91 – 152]:

(3.17)

Корни кубического уравнения являются главными напряжениями σ₁, σ₂, и σ₃. Для определения компонентов тензора главных напряжений можно воспользоваться выражением [86, с. 91 – 152]:

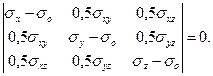(3.18)

Известно, что для главных напряжений выполняется следующее соотношение [86, с. 91 – 152]:

σ₁ ≥ σ₂ ≥ σ₃.

Интенсивность напряжений σ_инт можно вычислить по формуле [86, с. 91 – 152]:

σ_инт = МАХ (|σ₁ − σ₂| · |σ₂ − σ₃| · |σ₃ − σ₁| ). (3.19)

Эквивалентное напряжение σ_экв можно рассчитать по формуле [86, с. 91 – 152]:

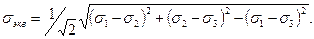(3.20)

Эквивалентные напряжения и деформация связаны между собой следующим соотношением [86, с. 91 – 152]:

σ_экв = 2ε_экв·G, (3.21)

где G = E /(2·(1 + ν)) – модуль сдвига;

Е – модуль Юнга;

ν – коэффициент Пуассона.

Напряжение текучести σ_у при текущей температуре вычисляется на первом шаге решения по времени [86, с. 91 – 152]. Затем на основе значений пробных деформаций определяются напряжения, которые представляют собой общую деформацию за вычетом пластической, полученной в предшествующий момент времени:

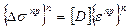(3.22)

Далее вычисляется эквивалентное напряжение σ_экв по формуле (3.20) [86, с. 91 – 152]. Металл остается упругим при выполнении условия σ_экв < σ_y. В таком случае приращения пластической деформации не вычисляются.

Когда эквивалентное напряжение превышает предел текучести, используя итерационную процедуру Ньютона-Рафсона, вычисляется пластический множитель λ [86, с. 91 – 152]:

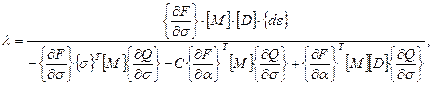(3.23)

где F – критерий текучести;

Q – пластический потенциал (определяет направление пластических деформаций);

α – смещение поверхности текучести;

С – трансляционный множитель;

[M] – матрица согласования;

Т – знак транспонирования матрицы.

Вектор приращения пластической деформации вычисляется по формуле [86, с. 91 – 152]:

(3.24)

Вектор текущей пластической деформации модифицируют, используя уравнение [86, с. 91 – 152]:

{ε^пл}ⁿ = {ε^пл}^{n − 1} + {Δε^пл}, (3.25)

и определяют упругую деформацию:

{ε^упр} = {ε^пр}ⁿ − {Δε^пл}. (3.26)

После этого вычисляется вектор упругих напряжений {Δσ^упр}ⁿ по формуле (3.13), а расчет приращение пластической работы производят по формуле [86, с. 91 – 152]:

Δχ ={σ^упр}ⁿ ·|M| · {Δε^пл}. (3.27)

Положение центра поверхности текучести определяют по формуле [86, с. 91 – 152]:

{Δα} = C{Δε^пл}. (3.28)

Текущие значения приращения пластической работы положения центра поверхности текучести обновляется по формуле [86, с. 91 – 152]:

χⁿ = χⁿ⁻¹ + Δχ и {α}ⁿ = {α}ⁿ⁻¹ + {Δα}, (3.29)

где верхний индекс n относится к шагу по времени.

Приращение эквивалентной пластической деформаций вычисляется по формуле [86, с. 91 – 152]:

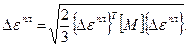(3.30)

В конце рассчитывают эквивалентное напряжение σ_экв по формуле (3.21), а для расчета эквивалентной пластической деформации {Δε^пл} используют следующее уравнение [86, с. 91 – 152]:

{Δε^пл} ={ε^пл}ⁿ − {ε^пл}ⁿ⁻¹. (3.31)

Таким образом, зная компоненты векторов напряжений и деформации, можно определить НДС и внешние нагрузки, действующие на деформируемую заготовку [86, с. 91 – 152].

В диссертационной работе была поставлена задача - провести имитационное моделирование и рассчитать НДС заготовки при прокатке в продольно-клиновом стане.

Популярный CAE-пакет «MSC.SuperForge» был выбран в качестве инструмента моделирования и расчета НДС. В настоящее время универсальный программный комплекс «MSC.SuperForge» является одним из лидеров программных комплексов автоматизированного инженерного анализа.

3.4 Основные положения метода конечных элементов, используемые в программном комплексе «MSC.SuperForge»

Известно [84, с. 65 - 213, 20, с. 76], что метод конечных элементов положен в основу программного комплекса «MSC.SuperForge». При этом в этой программе для различных областей деформируемого тела решаются известные формулы теории ОМД и теплопроводности совместно с начальными и граничными условиями в напряжениях, перемещениях или смешанного типа. В данной программе при решении математических задач ОМД используются следующие основные уравнения и соотношения [80, с. 39 - 134, 81, с. 31 - 112]:

1. Дифференциальные уравнения равновесия:

или 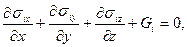(3.32)

где G_i – сила, приходящаяся на единицу объема.

В теории пластичности объемную силу приравнивают силе инерции, поэтому

G_i = - a _i ρ,

где ρ - плотность (кг/м³);

а_i – ускорение на i – ом шаге деформирования.

Ускорение определяют по формуле:

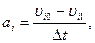(3.33)

где υ_i0 и υ_i1 - скорости в начале и конце каждого деформационного шага (м/с);

Δt - продолжительность i – ого этапа деформирования (с).

2. Формулы, позволяющие с помощью вектора перемещений определить компоненты тензора деформации (дифференциальные уравнения Коши):

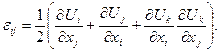(3.34)

3. В матричном виде распределение скорости конечных элементов можно записать в виде

(3.35)

где [N] - функция формы элемента;

{ ν_e } - вектор узловых скоростей.

Путем дифференцирования можно получить уравнение, позволяющее определить компоненты тензора скоростей деформации:

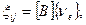(3.36)

где [B] - матрица, связывающая компоненты тензора скоростей деформации с компонентами узловых скоростей.

4. Условие пластичности Губера-Мизеса определяется по формуле:

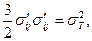(3.37)

где σ'_ij - девиатор напряжений;

σ_т - предел текучести.

5. Для деформируемой среды уравнение теплового баланса можно записать в виде

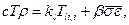(3.38)

где с – удельная теплоемкость среды при постоянном объеме;

Т – средняя абсолютная температура сплошной среды в градусах Кельвина;

k_l - коэффициенты, определяющие условия теплообмена на границе l ;

T_li,i – тепловое поле на границе l;

β - коэффициент, определяющий тепловыделение в результате деформации сплошной среды;

6. Накопленную деформацию определяют по формуле:

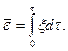
7. В большинстве случаев используют определяемый по формуле закон трения Кулона-Амонтона (касательные напряжения на поверхности контакта деформируемой среды с валком пропорциональны нормальным напряжениям):

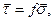(3.39)

где f – коэффициент трения.

8. Упругопластические и жесткопластические задачи ОМД могут решаться с помощью программного комплекса «MSC.SuperForge». При этом используются различные реологические модели в зависимости от вида решаемых задач.

В случае решения упругопластических задач для зон, находящихся в упругом состоянии, для определения связи между деформациями и напряжениями используют обобщенный закон Гука [80, с. 39 - 134, 81, с. 31 - 112], т.е.

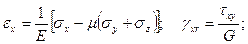
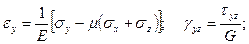(3.40)

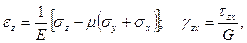
где Е – модуль Юнга;

G – модуль сдвига;

μ - коэффициент Пуассона.

Данные величины связаны между собой уравнением [80, с. 39 - 134, 81, с. 31 - 112]:

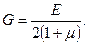(3.41)

Для зон деформируемой пластически, используют переменные параметры упругости Е^* и G^* [80, с. 39 - 134, 81, с. 31 - 112]. Тогда уравнения связи между деформациями и напряжениями записывают аналогично уравнениям (3.40), при этом используют уравнение подобное (3.41), т.е.

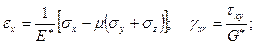
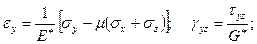(3.42)

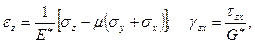
При исследовании процессов горячей прокатки решается жесткопластические задачи [80, с. 39 - 134, 81, с. 31 - 112]. Поэтому используют реологическую модель деформируемой среды, у которой напряжение течения зависят от степени деформации, скорости деформации и температуры, т.е.

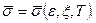(3.43)

Для аппроксимации уравнения (3.43) аналитическими зависимостями в теории пластичности используют известные эмпирические зависимости [80, с. 39 - 134, 81, с. 31 - 112]. Однако данные уравнения обладают определенными погрешностями и точно не определяют количественный и качественный характер зависимости (3.43). Поэтому в программе «MSC.SuperForge» не используются эмпирические уравнения. На основе экспериментальных данных, представленных в виде таблиц, осуществляют аппроксимацию сопротивления деформации в зависимости от термомеханических параметров деформирования.

9. Вариационный принцип Лагранжа используют в МКЭ и применяют в программном комплексе «MSC.SuperForge». Согласно данному принципу истинное состояние системы отличается от всех возможных тем, что сообщает полной энергии деформации минимальное значение [21, р.33 - 35, 24, р.15 - 186].

Расчеты производят поэтапно [87-90]. На каждом шаге расчета величину перемещений, деформаций и напряжений определяют по уравнениям:

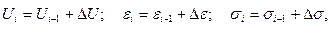(3.44)

где U_i-1, ε_i-1, σ_i-1 – значения перемещений, деформаций и напряжений на предыдущем шаге.

Минимум функционала полной энергии деформации на предыдущем этапе должны обеспечивать параметры U_i-1, ε_i-1, σ_i-1 [87, с.504 – 509, 88, с. 753 – 757, 89, с. 71 – 75, 90, с. 483 – 486]. Поэтому задача сводится к определению приращений функций ΔU, Δε, Δσ. При данных приращениях функционал также должен имеет минимальную величину.

На некотором шаге деформирования, описывающий полную работу деформации, функционал определяется уравнением [87, с.504 – 509, 88, 753 – 757, 89, с. 71 – 75, 90, с. 483 – 486]:

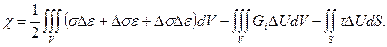(3.45)

Функционал (3.45) состоит из следующих слагаемых [87, с.504 – 509, 88, с. 753 – 757, 89, с. 71 – 75, 90, с. 483 – 486]: работу внутренних сил представляет собой первое слагаемое, работу массовых сил – второе слагаемое, работу поверхностных сил (сил трения) – третье слагаемое.

Через матричные и векторные составляющие (матрица базисных функций элементов, вектор узловых перемещений и т.п.) выражается функционал (3.45) [87, с.504 – 509, 88, с. 753 – 757, 89, с. 71 – 75, 90, с. 483 – 486]. При этом интегралы заменяются суммами и задача сводится к решению систем линейных уравнений относительно перемещений. Перемещения U, компоненты тензора деформации ε, компоненты тензора скорости деформации ξ, компоненты тензора напряжения σ, интенсивность деформаций, интенсивность напряжений, силы нормального давления, силы трения на поверхности контакта металла с валком, распределение температуру по объему заготовки (температурные поля) и другие параметры рассчитывается по найденным значениям ΔU₁,ΔU₂,..., ΔU_n.

Моделирование исследуемого процесса с использованием программного комплекса «MSC.SuperForge» осуществляется следующим образом [87, с.504 – 509, 88, с. 753 – 757, 89, с. 71 – 75, с. 90, с. 483 – 486]:

1. в зависимости от условий обработки (форма исходной заготовки и форма прокатываемого изделия, форма валка, условия деформирования и т.п.) выбирают тип конечно-элементного анализа, т.е. определяется, какая задача решается (плоская, осесимметричная или объемная);

2. создают геометрические модели исходной заготовки, валка и стана;

3. наносят сетку конечных элементов на заготовку;

4. используя либо имеющуюся в программе «MSC.SuperForge» базу данных, либо термомеханические свойства материала заготовки задают реологические свойства заготовки;

5. задают температуру, при которой начинается процесс прокатки заготовки;

6. задают условия на поверхности контакта заготовки и валка, т.е. коэффициент трения;

7. в зависимости от типа применяемого стана устанавливают закон движения подвижного инструмента;

8. с достаточно жесткой точностью производят расчеты. При этом производят расчет перемещения U, компоненты тензора деформации ε, компоненты тензора скорости деформации ξ, компоненты тензора напряжения σ, интенсивность деформаций, интенсивность напряжений, сила нормального давления, сила трения на поверхности контакта металла с валком, распределение температуру по объему заготовки;

9. в виде полей распределения соответствующих параметров по объему деформированного тела представляют результаты расчета или в виде числовых значений представляют исследуемые параметры в узлах деформированной сетки.

Важнейшим этапом моделирования процессов ОМД является нанесение сетки конечных элементов. Потому, что от нанесения сетки зависят точность и объем расчетов. В зависимости от типа решаемой задачи (плоская, осесимметричная или объемная) в программном комплексе «MSC.SuperForge» используется сетка элементов с использованием треугольников, четырехугольников, тетраэдров, трехгранных призм (пятигранников), шестигранников.

В зависимости от заданных условий, программный комплекс «MSC.SuperForge» имеет возможность автоматически разбивать деформируемый объем на необходимое количество элементов. При этом можно изменять сетку в процессе моделирования. При моделировании возможно задавать различные типы элементов для обрабатываемого тела одной и той же формы (треугольники и четырехугольники, тетраэдры и шестигранники).

В программном комплексе «MSC.SuperForge» предусмотрена возможность изменять плотность сетки элементов в отдельных зонах обрабатываемой заготовки.

3.5 Методика расчета НДС при прокатке полос в продольно-клиновом стане с использованием программного комплекса «MSC.SuperForge»

Для разработки методики моделирования структурообразования сталей при прокатке в продольно-клиновом стане необходимо было исследовать НДС заготовки при прокатке в данном стане.

Предлагаемый процесс прокатки полос является чрезвычайно сложным процессом. Связано это с тем, что во время прокатки заготовка деформируется непрерывно в пяти клетях с валками уменьшающимися диаметром в направлении прокатки.

На первоначальном этапе моделирования, используя программный комплекс «Inventor», создавали виртуальные объемные модели стана, клетей, валков и заготовки.

В последующем объемные виртуальные модели стана, клетей, валков и заготовки была импортирована в CAE программу «MSC.SuperForge» и соответствующим образом размещали в программе.

Для исследования процесса прокатки в продольно-клиновом стане использовали прямоугольную заготовку размером 5×20×50 мм. Прокатку полос моделировали в трехмерной среде с разбиением заготовки на четырех узловые элементы (CTETRA). Для модели тонкого сляба потребовалось 2518 элементов и 3180 узла. Материал заготовки - сталь Ст3сп (аналог DIN C10). Из базы данных программного комплекса «MSC.SuperForge» задавали реологические свойства. При этом материал заготовки принимали изотропным упругопластическим с нелинейным упрочнением (BISO). Начальную температуру заготовки приняли равным 1100 ^оС. На поверхности валка с заготовкой коэффициент трения принимали равным 0,3. Валки рассматривали как абсолютно твердые тела.

Запускали программу «MSC.SuperForge». Шаговым методом рассчитывали перемещения U, компоненты тензора деформации ε, компоненты тензора скорости деформации ξ, компоненты тензора напряжения σ, интенсивность деформаций, интенсивность напряжений, сила нормального давления, распределение температур по объему заготовки. При этом для наглядности отображения результатов расчета взяли данные для четырех стадии в процентном отношении к полному времени деформирования, т.е. были выбраны следующие интервалы: первая стадия - 20, вторая стадия - 40, третья стадия - 60 и четвертая стадия - 80 процентов от полного времени деформирования.