Методика статистической оценки результатов эксперимента
Одним из важнейших элементов системы обеспечения качества листового проката является статистический метод количественной и качественной оценки механических свойств и структурных показателей получаемой продукции. При этом многократными измерениями полученные экспериментальные данные математически обрабатывают и оценивают точность проведения экспериментов [64, 65, 66].
Средний размер измеряемой величины 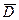 , дисперсия распределения
, дисперсия распределения 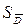 и среднеквадратичное отклонение по критерию Стьюдента определяют по формуле [65, с. 34 – 195]:
и среднеквадратичное отклонение по критерию Стьюдента определяют по формуле [65, с. 34 – 195]:
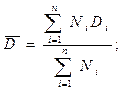 (2.1)
(2.1)
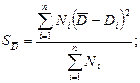 (2.2)
(2.2)
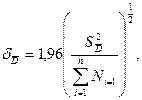 (2.3)
(2.3)
где Ni – число измерений в каждом опыте;
Di – размер измеряемой величины в каждом опыте;
n – число повторных опытов.
При проведении и обработке экспериментально полученных данных исследователи решают вопрос, связанный с включением в дальнейшую статистическую обработку грубые результаты, которые очень отличаются от всех других результатов. Делают проверку на попадание грубого результата в разряд больших ошибок. При возможности отбрасывают грубую ошибку эксперимента. При этом в большинстве случаев принимают, что ошибки измерения распределяются по нормальному закону распределения [66, с. 14 – 183].
Проверку попадания грубого результата в разряд больших ошибок осуществляют с помощью эмпирического стандарта [66, с. 14 – 183]:
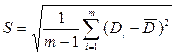 , (2.4)
, (2.4)
где 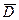 – среднее арифметическое значение экспериментальных данных
– среднее арифметическое значение экспериментальных данных 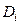 ;
;
m – количество измерений.
При этом определяют разность между «выскакивающим» значением 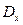 и средним значением
и средним значением 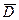 остальных (приемлемых) результатов, т.е. величину
остальных (приемлемых) результатов, т.е. величину 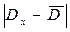 . Полученную величину делят на эмпирический стандарт и рассчитывают отношение:
. Полученную величину делят на эмпирический стандарт и рассчитывают отношение:
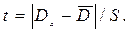 (2.5)
(2.5)
После расчета полученную величину t сравнивают с критическими значениями tn(P) (критерий Стьюдента) [66, с. 14 – 183]. Из данной работы известно, что в случае когда при заданном числе т приемлемых результатов отношение (2.5) оказывается больше критического, то экспериментально найденное значение содержит грубую ошибку и с надежностью Р можно грубое значение исключить из дальнейшей обработки результатов.
Дата добавления: 2014-12-22; просмотров: 910;
