Основы метода

Метод основан на простой формуле Байеса. Если имеется диагноз D_i и простой признак k_j, встречающийся при этом диагнозе, то вероятность совместного появления событий (наличие у объекта состояния D_i и признака k_j)

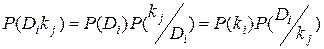. (3.1)

Из этого равенства вытекает формула Байеса

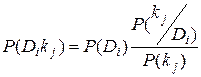. (3.2)

Очень важно определить точный смысл всех входящих в эту формулу величин. 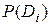- вероятность диагноза D_i, определяемая по статистическим данным (априорная вероятность диагноза). Так, если предварительно обследовано N объектов и у N_i объектов имелось состояние D_i, то

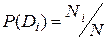. (3.3)

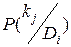вероятность появления признака k_j у объектов с состоянием D_i. Если среди N_i объектов, имеющих диагноз D_i у N_ij, проявился признак k_j, то

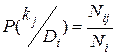. (3.4)

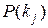- вероятность появления признака k_j во всех объектах независимо от состояния (диагноза) объекта. Пусть из общего числа N объектов признак k_j был обнаружен у N_j объектов, тогда

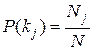. (3.5)

Для установления диагноза специальное вычисление 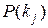не требуется. Как будет ясно из дальнейшего, значения 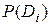, , 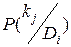известные для всех возможных состояний, определяют величину .

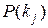В равенстве (3.2) 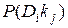- вероятность диагноза D_i после того, как стало известно наличие у рассматриваемого объекта признака k_j (апостериорная вероятность диагноза).

Обобщенная формула Байеса. Эта формула относится к случаю, когда обследование проводится по комплексу признаков K, включающему признаки k₁, k_2, …k_ν. Каждый из признаков k_j имеет m_j разрядов (k_j1, k_j2, …k_js, …, k_jmj). В результате обследования становится известной реализация признака 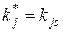и всего комплекса признаков K^*. Индекс * означает конкретное значение (реализацию признака). Формула Байеса имеет вид

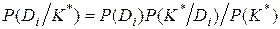, i=1, 2, …, n, (3.6)

где 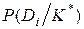- вероятность диагноза D_i после того, как стали известны результаты обследования по комплексу признаков К; 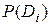- предварительная вероятность диагноза D_i (по предшествующей статистике).

Формула 3.6 относится к любому из n возможных состояний (диагнозов) системы. Предполагается, что система находится только в одном из указанных состояний и потому

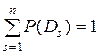. (3.7)

В практике нередко существуют несколько состояний A₁, …A_r, причем некоторые могут встретиться в комбинации друг с другом. Тогда в качестве различных диагнозов D_i следует рассматривать отдельные состояния D₁=A₁,…D_r=A_r и их комбинации D_r+1=A₁^A₂, … и т.п.

Если комплекс признаков состоит из ν признаков, то

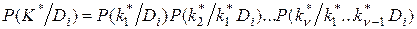, (3.8)

где 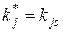- разряд признака, выявившийся в результате обследования.

Для диагностически независимых признаков

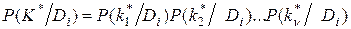. (3.9)

Вероятность появления комплекса признаков K^*

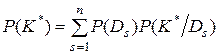. (3.10)

Обобщенная формула Байеса может быть записана

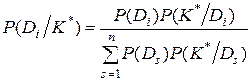, (3.11)

где 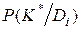определяется равенством 3.8 и 3.9.

Из соотношения 3.11 вытекает 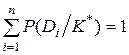, что, разумеется, и должно быть, так как один из диагнозов обязательно реализуется, а реализация двух диагнозов невозможна.