Алгоритмы диагноза и средства диагноза

Алгоритм диагноза задает совокупность элементарных проверок, последовательность их реализации и правила обработки результатов реализуемых элементарных проверок.

Результаты любой элементарной проверки могут быть использованы как признаки разбиения множества Е технических состояний объекта или подмножеств этого множества на классы. Любой алгоритм диагноза можно представить некоторым ориентированным графом. Ограничимся случаем, когда граф, представляющий алгоритм диагноза является деревом.

Дерево имеет вершины двух типов: вершины, из которых исходит хотя бы одна дуга, и вершины, из которых не отходит ни одной дуги.

Пример дерева дан на рис.6, где вершины первого типа представлены зачерненными кружками, а вершины второго типа – светлыми. В дереве имеется единственная вершина первого типа, в которую не заходит ни одна дуга. Эта вершина называется начальной, или корнем дерева (t₀, E). Вершины, из которых не исходит ни одной дуги, называются конечными, или висячими. Остальные вершины дерева называются внутренними. В каждую вершину дерева, кроме его корня, заходит только одна дуга. В дереве нет контуров.

Рангом вершины дерева называется число дуг пути, начинающегося в начальной вершине и заканчивающегося в рассматриваемой вершине. Минимальным рангом 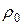дерева является ранг, для которого существует хотя бы одна висящая вершина и не существует ни одной висящей вершины ранга меньше 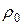. Максимальным рангом 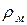дерева является ранг, для которого существует хотя бы одна вершина ранга 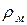и не существует ни одной вершины ранга больше .

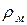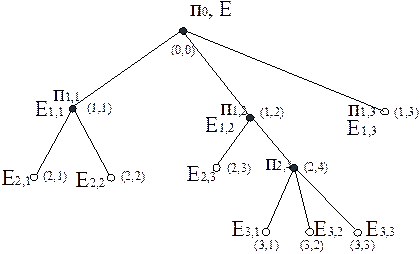
Рис. 6. Дерево алгоритма диагноза

Будем внутренние и висящие вершины дерева нумеровать парой чисел в скобках (ρ, σ), где ρ – есть ранг вершины, а σ – ее порядковый номер среди всех вершин одного и того же ранга (например, слева направо). Начальную вершину будем обозначать парой (0,0). Начальной и внутренней вершине сопоставим элементарные проверки множества П. Дугам дерева, исходящей из некоторой его вершины, сопоставим возможные результаты проверки, представляемой этой вершиной. Начальной вершине поставим в соответствие множество Евозможных технических состояний объекта, а внутренним и висящим вершинам – подмножества технических состояний, получаемые как классы разбиений по результатам соответствующих элементарных проверок. 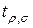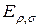Элементарную проверку и подмножество технических состояний, сопоставляемые вершине (ρ, σ) дерева будем обозначать символами и соответственно. Множество элементарных проверок 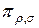обозначим символом П_д. Из правил построения дерева следует, что объединение множества технических состояний есть множество Евозможных технических состояний. Каждому пути соответствует последовательность элементарных проверок.

Рассмотрим, как дерево представляет алгоритм диагноза. Начальной вершине соответствует элементарная проверка 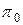множество Е всех возможных технических состояний. Элементарная проверка имеет три возможные результата, и тем самым разбивает множество Е на три подмножества Е_1,1, Е_1,2, Е_1,3 не различаемых этой проверкой технических состояний. Первые два из этих подмножеств соответствуют внутренним вершинам (1,1) и (1,2) и подлежат дальнейшим разбиениям элементарными проверкам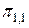и и 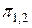. Третье подмножество соответствует висящей вершине, и поэтому разбиение его на подмножества алгоритмом не предусмотрено. Аналогично можно рассмотреть любую другую вершину дерева. Как только в процессе элементарных проверок будет достигнута висящая вершина, алгоритм диагноза прекращается. Фактическое техническое состояние объекта принадлежит подмножеству, соответствующему достигнутой висящей вершине. Каждой конкретной реализации алгоритма диагноза соответствует единственный путь. Например, если фактическое техническое состояние принадлежит подмножеству Е_3,2, то последовательность реализации элементарных проверок будет , , .

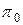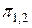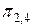Рассмотрим некоторый ненулевой ранг дерева. В общем случае дерево может иметь несколько внутренних вершин. Это значит, что возможны две разные последовательности реализации элементарных проверок. Обе эти проверки могут являться как одной и той же элементарной проверкой 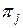множества П, так и разными элементарными проверками последнего. Если для каждого ранга дерева выполняется условие, состоящее том, что всем внутренним вершинам этого ранга сопоставлена одна и та же элементарная проверка из множества П, то алгоритм диагноза называется безусловным. Это соответствует заданию одной фиксированной последовательности реализации элементарных проверок из множества П, не зависящей от фактического технического состояния объекта. Т.е. выбор или назначение очередной элементарной проверки в последовательности их реализации не зависит от результатов предыдущих уже реализованных элементарных проверок. Если же в дереве найдется хотя бы один ранг с несколькими внутренними вершинами, которым сопоставимы разные элементарные проверки из множества П, то алгоритм диагноза называется условным. В условных алгоритмах выбор или назначение некоторых или всех (кроме 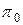) элементарных проверок производится с учетом результатов предыдущей уже реализованной элементарной проверки.

Достоинства безусловных алгоритмов: простота проверок, требуется хранить лишь состав элементарных проверок и единственную последовательность их реализации. Для условных требуется хранить кроме состава элементарных проверок все признаки безусловных и условных переходов от данной элементарной проверки к следующей, т.е. хранить не одну, а несколько последовательностей реализации элементарных проверок.

Безусловные алгоритмы диагноза можно классифицировать по характеру их остановки. Если выдача результатов диагноза предусмотрена только после реализации всех элементарных проверок, то алгоритм является алгоритмом с безусловной остановкой. Таким алгоритмам соответствуют деревья, у которых все висящие вершины имеют один и тот же ранг.

Во многих случаях фактическое техническое состояние объекта может быть определенно с требуемой глубиной диагноза прежде, чем будут реализованы все элементарные проверки алгоритма диагноза. Безусловные алгоритмы, у которых предусмотрена возможность выдачи результатов диагноза после реализации каждой элементарной проверки, называются алгоритмами с условной остановкой. Характерная особенность - не менее двух висящих вершин, ранги которых различны. Все условные алгоритмы являются алгоритмами с условной остановкой. Все указанные типы алгоритмов применяются в системах тестового диагноза. В системах функционального диагноза применяются алгоритмы с условной остановкой в связи с необходимостью немедленного определения неисправного состояния объекта.

Различают аппаратурные, программные и программно-аппаратурные средства диагноза (рис.7).

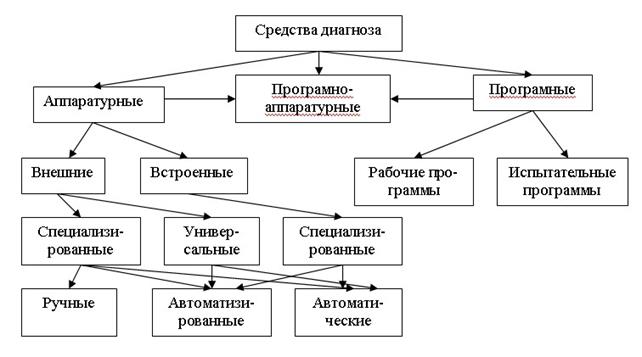
Рис. 7. Классификация средств диагноза

Под средствами диагностирования понимается совокупность технических устройств, предназначенных для съема, преобразования, хранения и представления (документирования, индикации) диагностической информации о контролируемых объектах.

В общем случае средства диагностирования позволяет решать следующие задачи технической эксплуатации:

- оценивать техническое состояние оборудования на различных этапах эксплуатации;

- определять место и причину отказа;

- контролировать правильность функционирования оборудования;

- накапливать и анализировать информацию о надежности с целью разработки и реализации мероприятий, направленных на поддержание надежности на заданном уровне, а также - с целью прогнозирования технического состояния.

Рекомендованная литература:[1,4,6,8]