Создание чертежа в трехмерной системе
При создании чертежей, связанных с построением различных поверхностей, целесообразно использование трехмерных систем. Поверхности образуются различными способами. Для целей компьютерной графики они могут быть разделены по способу получения: на элементарные геометрические поверхности, поверхности вращения, аналитические поверхности и поверхности произвольных форм.
Создание поверхностей методами твердотельного моделирования является наиболее наглядным и удобным.
Один из методов твердотельного моделирования основан на построении модели из набора базовых твердотельных примитивов, находящихся в библиотеках системы. Каждый примитив определен некоторой формой (цилиндр переменного сечения, параллелепипед и т.д.), точкой привязки, исходной ориентацией и изменяемыми размерами.
Объемные примитивы образуются путем выполнения такого перемещения плоской фигуры в пространстве, след от которого определяет форму примитива (например, поворот окружности вокруг оси образует сферу, а смещение многоугольника – призму).
Общепринятым порядком моделирования твердого тела (здесь поверхности) является последовательное выполнение булевых операций (объединения, вычитания и пересечения) над объемными примитивами (сферами, призмами, цилиндрами, конусами, пирамидами и т.д.). булевы операции базируются на понятиях алгебраической теории множеств.
Операция объединения (È) определяет пространство внутри внешней границы составной фигуры, полученной из двух тел, и результирующую составную фигуру как один элемент.
Операция вычитания (–) определяет пространство, оставшееся от одной фигуры после вычитания общей области двух фигур.
Операция пересечения (Ç) определяет пространство внутри границ общей области фигур.
Плоская фигура, на основе которой образуется тело, называется эскизом, а формообразующее перемещение эскиза — операцией.
Эскизизображается на плоскости. Для того, чтобы увидеть изображение проекционных плоскостей, их нужно выделить в Дереве построения. Плоскости показываются на экране условно – в виде прямоугольников, лежащих в этих плоскостях. Такое отображение позволяет пользователю увидеть расположение плоскости в пространстве. Положение плоскостей определяет существующая система координат.
Эскиз создается стандартными средствами графического редактора. При этом доступны все команды построения и редактирования изображения, команды параметризации и сервисные возможности. Как правило, эскиз представляет собой сечение объемного элемента. Реже эскиз является траекторией перемещения другого эскиза – сечения. Эскиз может располагаться в одной из ортогональных плоскостей координат, на плоской грани существующего тела или во вспомогательной плоскости, положение которой может задаваться пользователем.
Операции. Создание поверхности начинается с создания базового тела посредством выполнения операции над эскизом (или несколькими эскизами). При этом доступны следующие типы операций: вращение эскиза вокруг оси, лежащей в плоскости эскиза; выдавливание эскиза в направлении, перпендикулярном плоскости эскиза; кинематическая операция – перемещение эскиза вдоль указанной образующей; построение тела по нескольким сечениям эскиза.
После создания базового тела производится приклеивание или вырезание дополнительных объемов. Каждый из них представляет собой тело, образованное при помощи перечисленных операций над новыми эскизами. При выборе типа операции нужно сразу указать, будет ли тело вычитаться из основного объема или добавляться к нему.
Эскиз может быть построен на плоскости, в том числе на любой плоской грани тела.
Иногда при построении тела требуется произвести несколько одинаковых операций. Для их повторения используются разнообразные способы копирования.
Для выполнения некоторых операций требуется указание оси или направляющей. Если существующих в модели ортогональных плоскостей, граней и ребер недостаточно для построений, можно создать вспомогательные плоскости, оси и пространственные кривые, задав их положение одним из предусмотренных системой способов. Так, ось можно провести через три вершины или через ребро и вершину. Возможны и другие способы задания положения вспомогательных плоскостей.
Применение вспомогательных секущих плоскостей используется для построения линий пересечения любых математически определенных поверхностей с любым расположением в пространстве.
Созданную модель можно свободно перемещать и поворачивать мышью, если этому не препятствуют сопряжения.
Кроме твердотельных объектов в системах используются пространственные кривые: цилиндрические спирали; ломанные по точкам и координатам; сплайны[4] по точкам и координатам.
В обычном чертеже модели можно автоматически создать ассоциативные изображения трехмерной модели. Так, построение одной проекции можно сопровождать автоматическим синхронным построением второй, третьей, или второй и третьей проекций и аксонометрического изображения. Можно быстро построить большое число изображений при изменении размеров элементарных пересекающихся поверхностей и исследовать выявляющиеся при этом закономерности. Пользователь может разрушить проекционную связь в любой момент работы с документом. Все указанные изображения связаны с моделью: изменения в модели приводят к изменению изображения в ассоциативном виде.
Возможна демонстрация кинематических способов образования поверхностей, как на ортогональных проекциях, так и в аксонометрии с изменением параметров определителя поверхности.
Применение цвета повышает наглядность изображений, позволяет одновременно изображать различные слои или сечения.
10.7. Примеры решения некоторых типовых задач
начертательной геометрии методами компьютерной графики
Решение задач начертательной геометрии методами компьютерной графики является, безусловно, наглядным. Однако, для этого требуются базовые знания как самого предмета, так и навыков работы с графическими системами. Кроме того, каждая графическая система обладает, наряду со стандартными приемами работы, присущими среде Windows, и индивидуальными особенностями конкретной системы. С другой стороны, преемственность и аналогия современных программных продуктов позволяет достаточно быстро и легко осваивать новые графические системы.
Описанные ниже примеры реализованы в системе КОМПАс 5.10, выбор которой обусловлен простотой в усвоении и доступностью для целей обучения. для решения задач использовался графический редактор КОМПАс-графики подсистема КОМПАс-3d.
Пример построения линии пересечения плоскости и прямой. Решение задачи построения точки пересечения прямой и плоскости (рис. 10.1) является традиционной в начертательной геометрии.
Для построения искомой точки пересечения необходимо выполнить следующие действия:
1. По значениям координат точек построить в проекционной связи плоскость, заданную треугольником АВс, и прямую l.
2. Построить вспомогательную плоскость a.
3. Построить проекции линии пересечения вспомогательной плоскости с заданной плоскостью треугольника. На чертеже это линия показана проекциями точек 1, 2.
4. В пересечении построенной линии с прямой l находим на горизонтальной проекции искомую точку М.
5. Построить недостающую фронтальную проекцию точки М.
6. Используя конкурирующие точки 2 (3) и 4 (5), определяем видимость прямой относительно заданной плоскости.
7. Невидимые участки прямой линии показать штриховой линией.
Пример построения линии пересечения криволинейных поверхностей.
Для построения линии пересечения могут использоваться следующие типы операций:
- вращение эскиза вокруг оси, лежащей в плоскости эскиза;
- выдавливание (приклеивание) эскиза в направлении, перпендикулярном плоскости эскиза;
- кинематическая операция – перемещение эскиза вдоль указанной направляющей;
- построение тела по нескольким сечениям эскиза.
Каждая операция имеет дополнительные опции, позволяющие варьировать правила построения модели тела.
Построение линии пересечения кривых поверхностей методом твердотельного моделирования продемонстрировано на примере, представленном на рис.10.2.
 |
Рис. 10.1
 |
Рис. 10.2
1. Для создания твердотельной модели тора используется операция вращения контура сечения вокруг оси. Ось вращения выполняется примитивом «отрезок» стилем линии «осевая». Контур[5] выполняется при помощи примитива «окружность» стилем линии «основная».
2. Для создания цилиндрической поверхности используется операция выдавливания предварительно построенного цилиндра.
3. Автоматически построенные линии пересечения отображаются на экране при указании курсором мыши на проекции заданных поверхностей. Все проекции построенных моделей и линии пересечения создаются в проекционной связи.
Этот прием можно применять при построении линии пересечения для сферических, тороидальных, цилиндрических и конических (полных и усеченных) поверхностей. Примеры построения линий пересечения для других поверхностей продемонстрировано на рис. 10.3 и 10.4.
Игровые упражнения для развития пространственного представления.
Современные системы компьютерной графики обладают широкими возможностями для интенсификации процесса обучения инженерной графики и начертательной геометрии. Методы пространственного геометрического моделирования позволяют создавать каркасные, поверхностные и твердотельные модели. Возможности полутонового изображения модели позволяют учитывать оптические свойства ее поверхности (цвет, блеск, диффузия и др.); отображение модели в виде каркаса – совокупности всех ребер и линии очерка модели; отображение невидимых линий (ребер, частей ребер) и др.
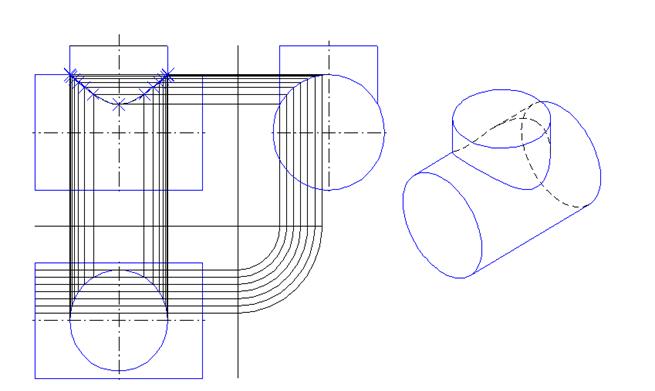
Рис. 10.3
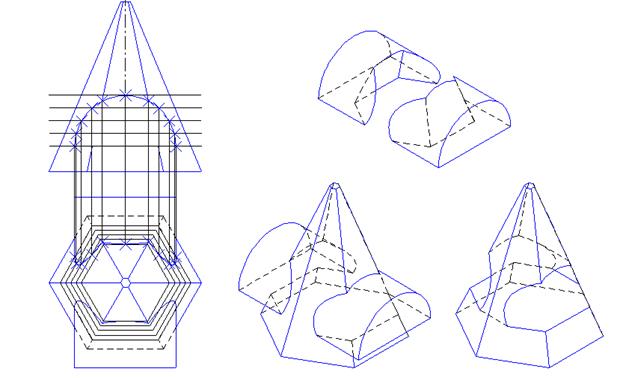
Рис. 10.4
На рис. 10.5 и 10.6 показаны различные возможности отображения поверхностей: отображение модели в виде каркаса с невидимыми линиями, полутоновое изображение.
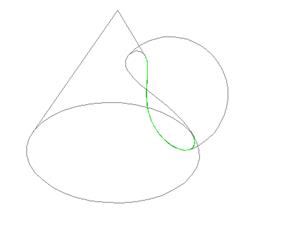
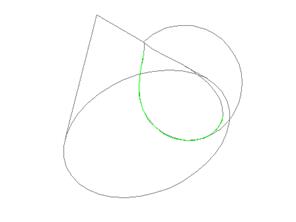
Рис. 10.5
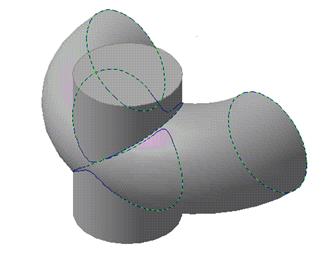
Рис. 10.6
Специальные команды позволяют выполнять различные динамические повороты изображения модели: вокруг точки (вершины, центра сферы); вокруг вертикальной (горизонтальной) плоскости, перпендикулярной плоскости экрана, вокруг оси или прямолинейного ребра и др.
Рекомендуемая литература
1. Гордон, В. О. Курс начертательной геометрии / В.О. Гордон, М. А. Семенцов-Огиевский. − М.:Высш.шк., 2008
2. Гордон, В.О. Сборник задач по курсу начертательной геометрии / В. О. Гордон, Ю. Б. Иванов, Т. Е. Солнцева. − М.: Высш.шк., 2007.
3. Королев, Ю.И. Начертательная геометрия: Учебник для вузов / Ю. И. Королев.- Спб.: Питер, 2007.
4. Фролов, А.С. Начертательная геометрия / А. С. Фролов. − М.: Высш. Школа,2002.
5. Чекмарев, А.А. Начертательная геометрия и черчение / А. А. Чекмарев: − М.: Гуманит .изд. центр ВЛАДОС, 2002.
6. Буланже, Г.В. Инженерная графика. Проецирование геометрических тел / Г. В. Буланже. – М.: Высш.шк.,2008.
7. Зайцев, Ю.А. Начертательная геометрия. Решение задач / Ю. А. Зайцев. – М.: Из-во Дашков и Ко, 2008.
8. Кирин, Е. М. Теоретические основы решения задач по начертательной геометрии: учеб. пособие / Е. М. Кирин, М. Н. Краснов. − Пенза: Изд-во Пенз.гос. ун-та, 2007.-148 с. : ил.
9. Лазарев, С. И. Начертательная геометрия для первокурсника: Учеб.пособие /С. И. Лазарев, Э. Н. очнев, О. А. Абоносимов. Тамбов: Изд-во Тамб. гос. техн. ун-та, 2004. 68 с.(эл. версия).
10. Локтев, О.В. Краткий курс начертательной геометрии / О. В. Локтев. – М.: Высш. Школа, 2006.
[1] «Через точку, лежащую вне данной прямой, можно провести только одну прямую линию, ей параллельную». «Сумма углов любого плоского треугольника равна двум прямым или 180°».
[2] Эти поверхности с большой натяжкой можно рассматривать как модели пространства Римана, которые помогут увидеть основные особенности геометрии Римана.
* Геодезическойназывается линия, принадлежащая поверхности и кратчайшая из всех линий, которые можно провести между двумя точками поверхности. Геодезическая линия изображается на развертке поверхности в виде прямой линии.
[3] Слой — уровень, на котором размещается часть объектов чертежа.
[4] Сплайн – плавная кривая, проходящая через заданный набор точек. Сплайны являются основой для поверхностей свободной формы.
[5] При работе в эскизе под контуром понимается любой линейный графический объект или совокупность последовательно соединенных линейных графических объектов (отрезков, дуг, сплайнов, ломаных и т.д.).
Дата добавления: 2014-12-18; просмотров: 1784;
