Развертка поверхности прямого кругового конуса
Развертка боковой поверхности конуса вращения (рис. 9.7) представляет сектор круга, радиус которого равен длине образующей конуса, а длина дуги равна длине окружности основания конуса.

Рис. 9.7
Обычно этот сектор строят по его центральному углу, величина которого j подсчитывается по формуле j = 360° 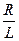 , где R – радиус основания конуса, L – длина его образующей.
, где R – радиус основания конуса, L – длина его образующей.
На рис. 9.8 изображена развертка боковой поверхности данного конуса.

Рис. 9.8
Для построения на развертке линии, по которой поверхность конуса пересекается плоскостью a, надлежит на его поверхности наметить ряд равномерно расположенных образующих (на рис. 9.7 их проведено 8), провести их на развертке и нанести на них точки, в которых каждая образующая пересекалась плоскостью a.
Отрезки S¢¢1¢¢ и S¢¢5¢¢ выражают истинные расстояния точек сечения 1 и 5 от вершины конуса. Остальные образующие должны быть предварительно повернуты вокруг оси конуса до положения, параллельного фронтальной плоскости проекций, при этом расстояния точек 2, 3, 4, 6, 7 и 8 от вершины конуса выразятся, соответственно, отрезками 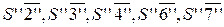 и
и 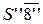 .
.
Длины этих отрезков откладываются на соответственных образующих развертки от точки S, и их конечные точки соединяются в последовательном порядке плавной кривой.
Дата добавления: 2014-12-18; просмотров: 1381;
