ГЕОМЕТРИЯ ПОВЕРХНОСТИ РАЗДЕЛА

Форма твердого вещества, вступающего в реакцию с жидкостью или газом, играет важную роль в определении скорости процесса. Если твердое вещество имеет форму пластинки или диска, то площадь поверхности в течение реакции будет неизменной, поэтому скорость реакции будет постоянной. При условии пренебрежения реакции на торцах. Если образец имеет форму цилиндра или шара, то по мере протекания реакции площадь поверхности и соответственно скорость реакции будет меняться.

Рассмотрим реакцию системы твердое тело – жидкость, например растворение металла в кислоте. Допустим, что концентрация кислоты остается постоянной в течение всей реакции, тогда

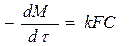(46)

где M- масса твердого тела в момент времени t; F – площадь его поверхности; С – концентрация кислоты; k - константа скорости.

Отрицательный знак показывает на убывании массы при растворении.

При изменении геометрии твердого тела получаются различные кинетические уравнения.

Плоский образец (пластинка).

Площадь поверхности F будет постоянна в течение всего процесса растворения:

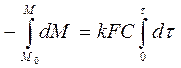, (47) и (48)

Следовательно, график зависимости M₀ – M от t должен быть прямой линией с наклоном равным kFC, из которого можно вычислить k.

Образец в форме шара.

Площадь поверхности будет убывать во времени:

(49)

где r – радиус, а r - плотность.

Следовательно:

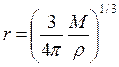и ,

, ,

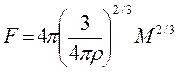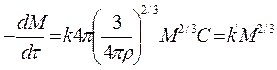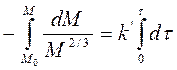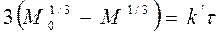(50)

Следовательно, график зависимости 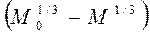от t или M^1/3 от t должен быть прямой линией.

Образец в виде цилиндра или проволоки.

Пренебрегая реакцией на концах и считая длину цилиндра или проволоки l= const, получим следующие уравнения:

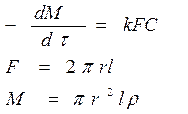(51)

Следовательно

, ,

, ,

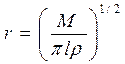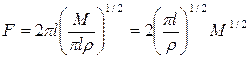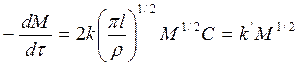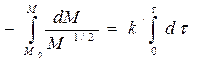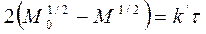(52)

Следовательно, график зависимости (M₀^1/2 – M^1/2) от t или M^1/2 от t должен быть прямой линией.

Образец в форме куба.

В этом случае используем уравнения:

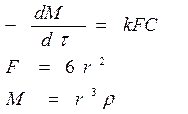(53)

Следовательно:

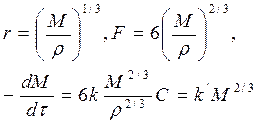(54)

Получаем уравнение такое же, как для шара.

Уравнения скорости, выраженные в прореагировавших долях.

Прореагировавшая доля (степень превращения) твердого вещества задается выражением 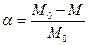. Кинетические уравнения для образцов различной формы приведены ниже:

1. Шар

,

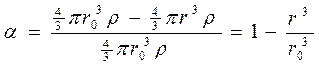Для расчетов используем уравнения (49). Получаем:

,

, , ,

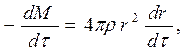
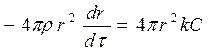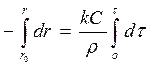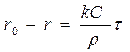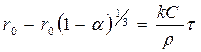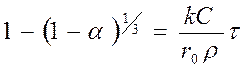(55)

График зависимости 1-(1- a)^1/3 от t дает прямую линию.

2. Куб

,

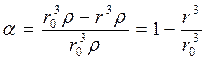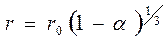
Для расчетов используем уравнение скорости (46). Получаем:

, ,

,

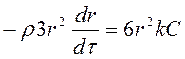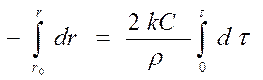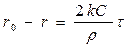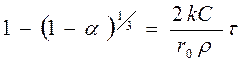(56)

Следовательно, график зависимости 1-(1- a)^1/3 от t дает прямую линию.

3. Цилиндр.

, .

,

, , ,

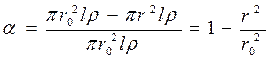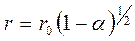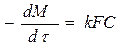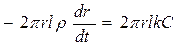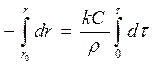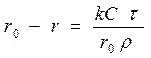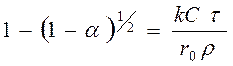(57)

Следовательно, график зависимости 1-(1- a)^1/2 от t дает прямую линию.