Способы задания поверхностей

Поверхность, образованная каким-либо способом, считается заданной, если относительно произвольной точки пространства можно однозначно решить вопрос о ее принадлежности данной поверхности. Для поверхности, заданной на чертеже, это условие становится следующим: поверхность считается заданной, если по одной проекции точки, принадлежащей поверхности, можно построить вторую проекцию. Совокупность условий, необходимых для задания поверхности, называется определителем поверхности. Он состоит из геометрической и алгоритмической частей. Геометрическая часть определителя – это перечень геометрических элементов и фигур, которые участвуют в образовании поверхности. Алгоритмическая часть определителя описывает взаимосвязи между элементами и фигурами, входящими в геометрическую часть, а также представляет совокупность правил, по которым образуется поверхность. Например, поверхность сферы можно образовать, вращая некоторую точку вокруг другой неподвижной точки (центра сферы) и поворачивая при этом плоскость вращения вокруг оси, проходящей через центр сферы. В этом случае в геометрическую часть определителя войдут две точки, а в алгоритмическую часть – описание правил вращения одной точки вокруг другой.

Следует иметь в виду, что при задании поверхности можно в ряде случаев вместо геометрических элементов задавать числовые параметры. Например, сферу можно было бы задать центром и величиной радиуса. Для задания конуса вращения необходимо определить ось вращения и величину угла между образующей конуса и осью. Такие параметры поверхности принято разделять на параметры формы и положения. Параметры, изменение которых приводит к изменению формы поверхности, называются параметрами формы. Если же при изменении параметра меняется положение поверхности в пространстве, то такой параметр относят к параметрам положения. В случае задания сферы ее радиус является параметром формы, а координаты центра сферы – параметрами положения. Число независимых параметров поверхности называется ее параметрическим числом.

Существует три наиболее распространённых способа задания поверхностей: аналитический, графический и графоаналитический. Рассмотрим каждый из этих способов.

Аналитический способ. В этом случае поверхность рассматривается как геометрическое место точек, координаты которых удовлетворяют заданному уравнению вида:

F(x, y, z) = 0или z = Ф(х, у),

где Fи Ф - алгебраическая или трансцендентная функция.

Поверхность также может задаваться системой уравнений, определяющих зависимость координат точек поверхности от некоторого параметра:

x = X(t)

z = Z(t).

Такой способ задания называется параметрическим.

Широкое распространение в последнее время получила векторная форма задания поверхности, в этом случае поверхность определяется вектор-функцией R некоторой точки N, принадлежащей поверхности. Эта функция зависит от двух скалярных аргументов u и v:

R = R(u,v) = x(u,v)i + y(u,v)j + z(u,v)k,

где x,y,z – координаты вектор-функции. Параметры u и v называются криволинейными координатами поверхности. Каждой паре значений u, v из области их изменения соответствует точка поверхности, координаты которой определяются функциями

x = x(u,v), y = y(u,v), z = z(u,v).

Если один из параметров принять постоянным, например, задаться v=v₁, то вектор функции R=R(u,v₁) опишет на поверхности некоторую линию v₁=const, называемую координатной линией. Переходя к другому значению v=v₂, получим следующую линию семейства v₂=const. Совокупность линий v_i=const (i=1, …, m) образует линейный каркас поверхности (линейным каркасом поверхности называется множество линий, заполняющих поверхность так, что через каждую точку поверхности проходит в общем случае одна линия этого множества).

Аналогично, фиксируя u и изменяя v, можно получить координатную линию u=const.Множество линий u_j=const (j=1, ..., n) образует другой линейный каркас той же поверхности. Через каждую точку поверхности можно провести две координатные линии (одну – семейства u_j=const, другую – v_i=const).Совокупность двух линейных каркасов образует сетчатый каркасповерхности или сеть.

Векторная форма задания поверхностей часто используется для задания кинематических поверхностей. Действительно, пусть образующая линия поверхности задана параметрически в виде r = r(u). Вводя второй параметр v, определяющий перемещение образующей в пространстве, можно получить сетчатый каркас поверхности, описывающийся уравнением r =r (u,v). Причем линии каркаса v_i = const в этом случае представляют собой семейство образующих, а линии каркаса u_j =const - семейство направляющих линий поверхности (рис.9.2).

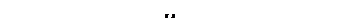
Рис.9.2

Графический способзадания поверхностей предполагает задание поверхности на комплексном чертеже. При этом, как уже было сказано выше, поверхность считается заданной, а ее чертеж – метрически определенным, если по одной проекции точки, лежащей на поверхности, можно построить другую ее проекцию. Чаще всего поверхность задается на чертеже проекциями элементов своего определителя, т.е. тех геометрических объектов, с помощью которых поверхность была образована. Алгоритмическая часть определителя поверхности переводится при этом в алгоритм графических и аналитических операций, которые необходимо осуществить над проекциями элементов определителя, чтобы построить проекции произвольных точек или линий поверхности. Однако наглядность такого чертежа поверхности очень низкая. Для улучшения наглядности чертеж поверхности приходится дополнять проекциями наиболее характерных или важных точек и линий поверхности, в том числе очерковымилиниями ее проекций. Очерковыми линиями (или очерком) проекций поверхности называются линии, ограничивающие области ее проекций (рис.9.3).

Рис.9.3

Часто поверхность задается на чертеже некоторой совокупностью ее точек (называемой точечным каркасом поверхности) или линий (линейный или сетчатый каркас). Например, поверхность, образованная кинематическим способом, может задаваться на чертеже проекциями семейства направляющих линий и семейства образующих линий. Однако в этом случае поверхность будет не вполне определена, так как между точками и линиями каркаса поверхность не задается. Поэтому построить промежуточные точки и линий поверхности можно лишь приближенно. Для придания однозначности чертежу поверхности обычно пользуются одним из двух способов:

1. Задается алгоритм графических операций перехода от заданных линий каркаса к промежуточным линиям.

2. С помощью аналитических методов аппроксимации и какого-либо класса моделирующих функций рассчитывают математическую модель поверхности, содержащую заданные точки и линии каркаса. Эту модель в дальнейшем используют для получения промежуточных точек и линий. Однако нужно иметь в виду, что точность результата во многом определяется выбранным классом моделирующих функций.

Графоаналитический способ. При этом способе задания поверхности часть линий (например, образующая поверхности) может задаваться аналитически в виде уравнения

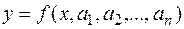
где 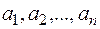– параметры образующей, а направляющие линии задаются графически, в виде графиков изменения параметров 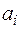в зависимости от значения третьей координаты z (рис.9.4). Тогда при необходимости получения положения некоторой образующей для 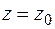определяют сначала значения параметров 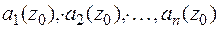, которые затем подставляются в уравнение образующей.

Рис.9.4