ПРАВИЛО ВЕРЕЩАГИНА ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ.

В 1924 году Верещегин предложил более простой способ вычисления интеграла Мора:

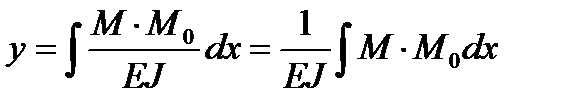
Для определения перемещений необходимо знать площадь эпюры моментов от внешней нагрузки и найти положение ее центра тяжести. Если эпюра моментов имеет сложную конфигурацию, то ее разбивают на простые площади w1,w…,wn , и находят положение центра тяжести для каждой площади. Строится эпюра моментов от единичной силы или единичного момента, в зависимости от того, что определяется у или Θ. Под центром тяжести эпюр моментов от внешней нагрузки берутся ординаты на эпюре моментов от единичных силовых факторов. Сумма произведений, отнесенная к жесткости рассматриваемого элемента, даст перемещение в данной точке.

.

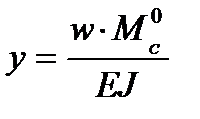Задача. Найти перемещение точки приложения сосредоточенной силы в консольной балке.

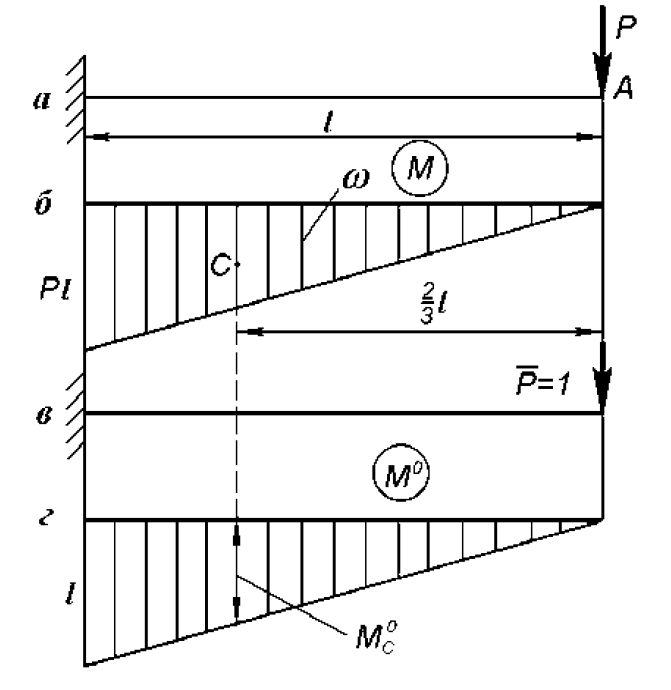
Строим эпюру моментов от силы Р и определяем ее площадь:

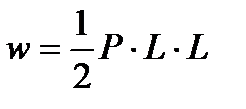
Строим эпюру моментов от единичной силы Р=1. Эта сила прикладывается в точке, в которой ищется перемещение по направлению действия заданной силы Р. Ордината под центром тяжести эпюры М на эпюре моментов от единичной силы равна 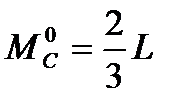. Перемещение точки будет равно:

.

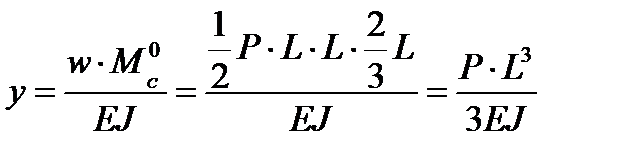Задача. Для двухопорной балки, нагруженной посередине пролета сосредоточенной силой Р, определить прогиб в точке приложения силы С, пользуясь интегралом Мора.

Построим дополнительную схему балки и приложим посередине пролета силу 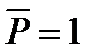. Опорные реакции основной и дополнительных схем соответственно равны: А = В = P/2 и А'= В' = 1/2.

Найдем изгибающие моменты в произвольном сечении:

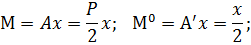
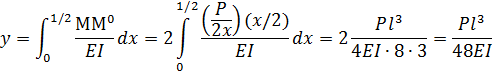
Коэффициент 2 перед интегралом введен в выражение ввиду того, что балка содержит два одинаковых участка.