ПОНЯТИЕ ЛИНЕЙНЫХ И УГЛОВЫХ ПЕРЕМЕЩЕНИЙ ПРИ ИЗГИБЕ.
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ УПРУГОЙ ЛИНИИ БАЛКИ.
Изогнутой осью балки или ее упругой линией называется кривая, в которую превращается прямолинейная ось балки после приложения к ней внешней нагрузки.
Плоский поперечный изгиб характеризуется двумя величинами:
- перемещением f центра тяжести сечения по направлению, перпендикулярному оси балки, которое носит название прогиба;
- углом Θ поворота сечения или равным ему углом наклона касательной к упругой линии.
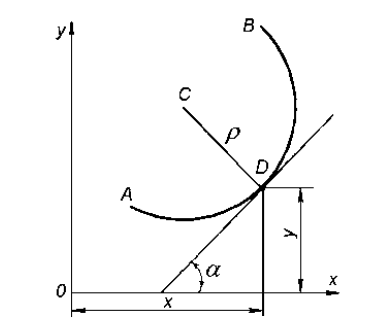
Из курса высшей математики известно, что кривизна кривой АВ в произвольной точке может быть выражена формулой:


При известном уравнении кривой 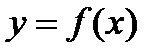 ее кривизна в каждой точке может быть вычислена через первую и вторую производные от этой функции.
ее кривизна в каждой точке может быть вычислена через первую и вторую производные от этой функции.
Математическую кривизну можно связать с кривизной балки при изгибе:
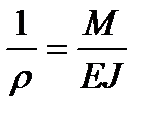
Кривизна балки прямо пропорциональна изгибающему моменту и обратно пропорциональна ее жесткости.
Приравняем правые части уравнений
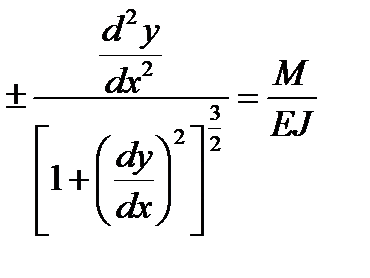
Если балка под действием внешних нагрузок имеет значительные перемещения, то дифференциальное уравнение используется для нахождения прогибов и углов поворота балки.
Учитывая, что современные конструкции обладают большой жесткостью, а величина прогиба незначительна по сравнению с длиной, уравнение можно упростить.
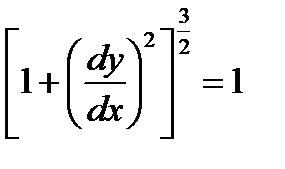
Основанием для этого является то, что изогнутая ось балки представляет собой весьма пологую линию. Следовательно, 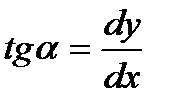 - величина, равная нулю, так как тангенс угла, образованного касательной к кривой
- величина, равная нулю, так как тангенс угла, образованного касательной к кривой 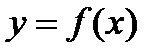 с осью Х,
с осью Х,
и есть 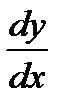
Вводя это допущение, получаем приближенное дифференциальное уравнение
изогнутой оси балки.
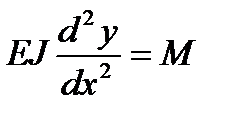
Если дважды проинтегрировать это уравнение, получим уравнение прогибов и углов поворота.

Постоянные интегрирования С и D определяются из граничных условий на концах каждого участка балки.
- для балок с защемленным концом прогиб и угол поворота в заделке равны нулю.
у=0; Θ =0, это граничные условия для определения С и D.
- для двух опорных балок прогибы в левой и правой опорах равны нулю
уА=0; уB =0, это граничные условия для определения С и D.
В 1875 году итальянским ученым Кастельяно была предложена теорема для определения прогибов и углов поворота балки, основанная на вычислении потенциальной энергии деформации.

Максвелл и Мор одновременно предложили способ определения линейного и углового перемещений, который состоит в том, что частные производные 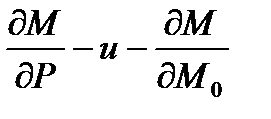 заменили действием в искомом сечении единичной силы
заменили действием в искомом сечении единичной силы 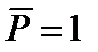 и единичного момента
и единичного момента 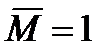 . Перемещения по теореме Максвелла и Мора при изгибе можно определить интегралом в виде
. Перемещения по теореме Максвелла и Мора при изгибе можно определить интегралом в виде
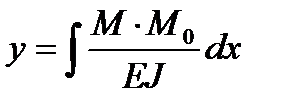
где: М- изгибающий момент в сечении балки от внешней нагрузки;
М0 – единичный момент от единичной силы или единичного момента в зависимости от того какое перемещение определяется – линейное или угловое.
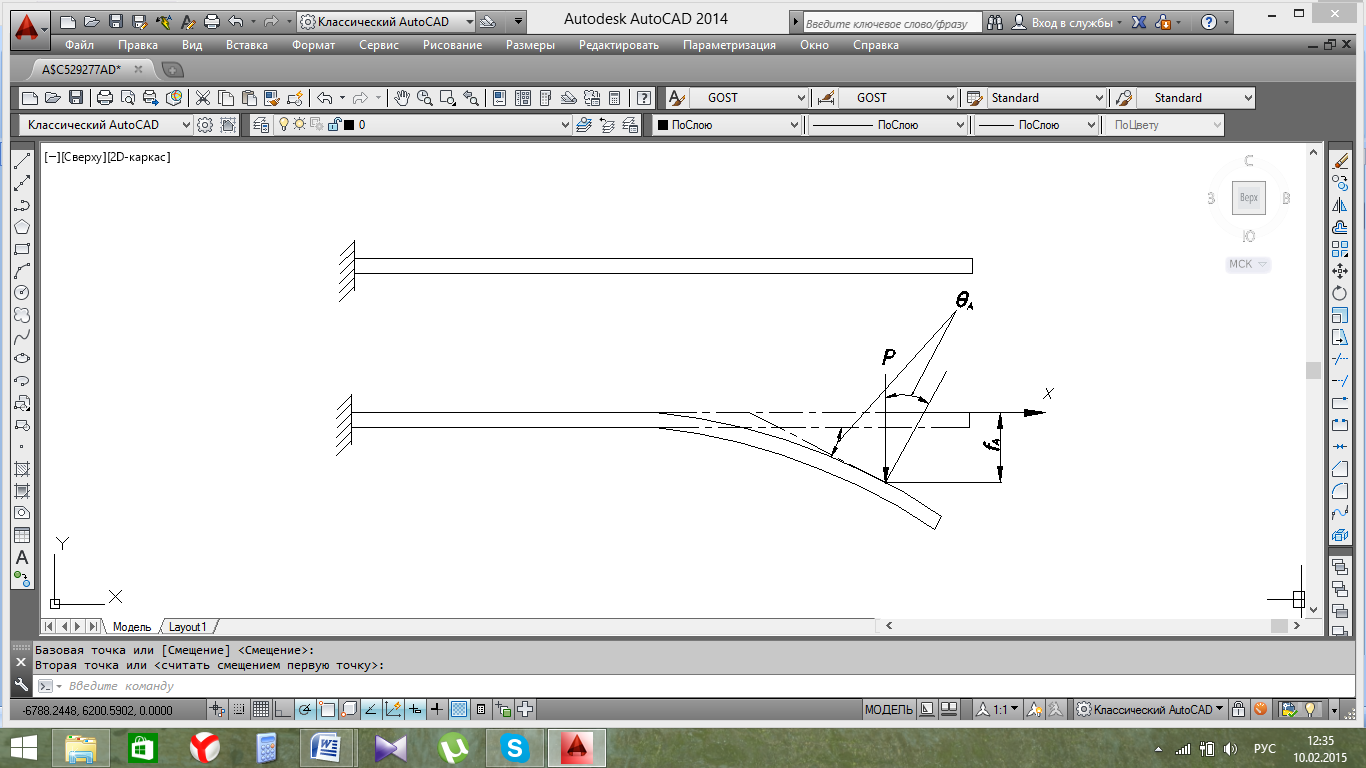
Рассмотрим консольную балку, нагруженную на конце сосредоточенной силой. Определить в точке приложения силы линейное и угловое перемещение.
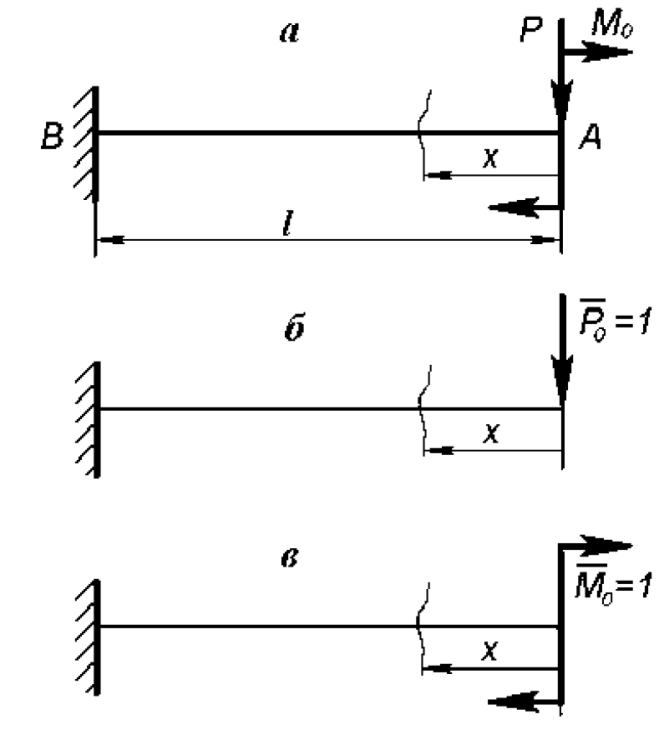
Для определения перемещений Уа и  а. Построим две дополнительные схемы балки (б) и (в) и приложим на конце одной единичную силу
а. Построим две дополнительные схемы балки (б) и (в) и приложим на конце одной единичную силу 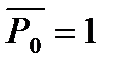 и единичный момент
и единичный момент 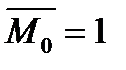
Найдем изгибающие моменты от всех нагрузок:

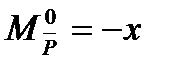

Используя формулы, получим значения для Уа и  а
а
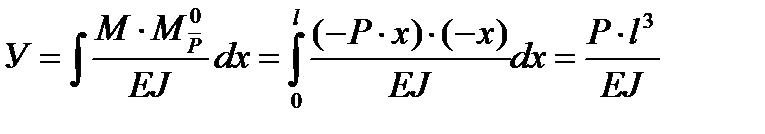
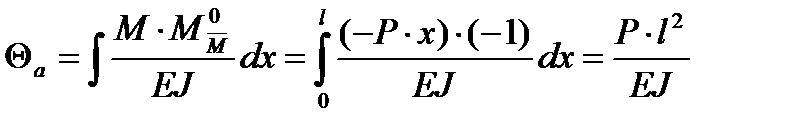 .
.
Дата добавления: 2017-03-29; просмотров: 3465;
