Г) Мс и М - линейные функции w.

Полученные в п.п. б) и в) результаты можно распространить на случай, когда М и М_с - линейные функции скорости.

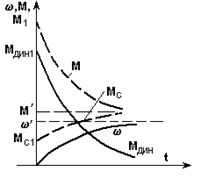
Рассмотрим эту возможность на простом примере. Пусть требуется рассчитать переходный процесс пуска привода, если характеристики двигателя и нагрузки заданы, как показано на рис. 5.10,а пунктиром.

а) б)

Рис. 5.10. Механические характеристики (а) и кривые переходных процессов (б)

при линейных зависимостях М(w) и М_с(w)

Заменим эти характеристики одной - зависимостью динамического момента М_дин = М - М_с от скорости. Эта зависимость линейна, так как линейны М(w) и М_с(w) - сплошная линия на рис. 5.10,а. Теперь, воспользовавшись полученными ранее результатами, можно получить зависимости w(t) и М_дин(t). При этом w_нач = 0, w_кон = w¢, М_{дин нач} = М_дин1, М_{дин кон} = 0, 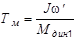; кривые построены на рис. 5.10,б сплошными линиями. Если необходимо, можно построить и графики М(t) и М_с(t), так как известны начальные и конечные величины (рис. 5.10,а) и определена Т_м. Эти графики показаны на рис. 5.10,б пунктиром.

5.3. Переходные процессы при L=0 и “медленных” изменениях воздействующего фактора

К задачам данной группы ранее были отнесены переходные процессы в системе преобразователь - двигатель (П-Д). Фактор, вызывающий переходный процесс, изменяется не мгновенно (темп его изменения соизмерим с темпом изменения скорости привода в переходном процессе); учитывается только механическая инерция в приводе (J), индуктивности в цепях двигателя малы или не проявляются.

Типичные структуры системы П-Д и соответствующие механические характеристики показаны на рис. 5.11 и 5.12.

а) б)

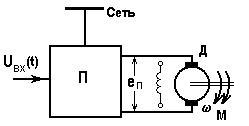
Рис. 5.11. Система ПН-ДПТ и ее механические характеристики

Роль преобразователя П в схеме на рис. 5.11, как отмечалось, может играть генератор (система Г-Д) или тиристорный преобразователь (ТП-Д). Фактор, вызывающий переходный процесс в этих системах, - изменение входного сигнала u_вх, приводящее к изменению ЭДС преобразователя е_п.

а) б)

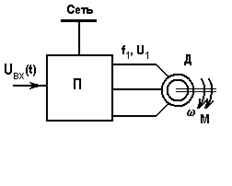
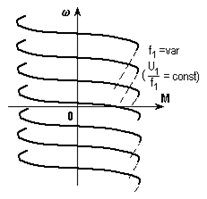
Рис. 5.12. Система ПЧ-АД и ее механические характеристики

Роль преобразователя П в схеме на рис. 5.12 играет статический преобразователь частоты. Фактор, вызывающий переходный процесс в этих системах, - изменение входного сигнала u_вх, приводящее к изменению частоты и напряжения на выходе преобразователя.

Как и прежде, целью изучения переходных процессов в системе П-Д будет определение зависимостей w(t), М(t) и иногда i(t) при известных условиях переходного процесса и параметрах привода.

Введем ряд условий и допущений.

1. Механические характеристики привода w(М) известны, линейны (по крайней мере, на рабочих участках) и параллельны друг другу, то есть выражаются уравнением (5.4):

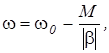
где - жесткость характеристик.

2. Известны или могут быть определены зависимости е_п(t) или f₁(t), то есть закон изменения во времени фактора, вызывающего переходный процесс. Так как е_п или f₁ однозначно связаны со скоростью идеального холостого хода привода w₀

- для схемы на рис. 5.11,

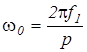- для схемы на рис. 5.12,

то известен закон изменения во времени w₀.

3. Известно начальное (w_нач, М_нач) и конечное (w_кон, М_кон) состояние привода, момент инерции J и момент сопротивления М_с = const.

4. Преобразователь П обладает двусторонней проводимостью, то есть характеристики w(М) могут располагаться во всех квадрантах плоскости w, М.

Рассмотрим прежде всего качественные отличия переходных процессов в системе П-Д от изученных ранее случаев, когда е_п или f₁ изменялись мгновенно, то есть мгновенно устанавливалась соответствующая новая механическая характеристика, а изменение скорости w и момента М в переходном процессе происходило согласно именно этой характеристике. Переходный процесс определялся статической механической характеристикой привода.

В рассматриваемых далее задачах е_п или f₁ изменяются, как указывалось, не мгновенно, то есть переход привода с одной характеристики на другую происходит постепенно, одновременно с изменением скорости, в результате чего соответствие между скоростью w и моментом М в каждый момент времени определяется не статической механической характеристикой, а другой, отличной от нее характеристикой, которую мы далее будем называть динамической механической характеристикой или просто динамической характеристикой.

В качестве примера на рис. 5.13 показана статическая характеристика асинхронного двигателя при номинальной частоте 1, по которой будет происходить пуск при мгновенном приложении к двигателю напряжения такой частоты, и динамическая характеристика 2, соответствующая пуску двигателя путем плавного изменения частоты от нуля до номинальной по некоторому закону.

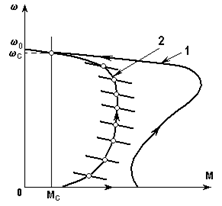
Рис. 5.13. Статическая 1 и динамическая 2 механические характеристики

Динамические характеристики определяются темпом изменения фактора, вызывающего переходный процесс, и параметрами привода, могут очень сильно отличаться от статических характеристик и даже иметь совсем другую форму.

Легко обнаружить связь зависимостей w(t) и М(t) с динамической характеристикой привода: исключив время t из уравнений w(t) и М(t), мы получим динамическую характеристику.