Процедуры поиска удовлетворительных значений критериев
Эти процедуры также предназначены для систематического поиска наилучшего решения. Однако такой поиск осуществляют по-иному: в порядке очереди определяют приемлемое значение по каждому из критериев.
Процедура «STEM» ЧМП поиска удовлетворительных значений критериев. Предназначена для решения многокритериальных задач линейного программирования, например многокритериальной транспортной задачи.
Фазы расчетов и анализа ЧМП «STEM».
Фаза расчета:
1. Проводится оптимизация по каждому критерию в отдельности, при этом значения всех остальных критериев заносятся в таблицу 4.
Таблица 4.
Относительные значения критериев
| Критерии | 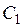
| 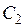
| … | 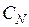
|
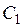
| 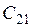
| 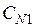
| ||
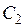
| 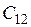
| 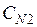
| ||
| … | … | … | … | … |
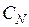
| 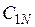
| 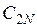
|
В таблице 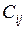 - значение i- го критерия при оптимизации по j- му критерию. Ясно, что диагональное элементы равны единице, а все прочие меньше единицы. Очевидно, что после нормировки наибольшее значение каждого критерия равно единице, а наименьшее нулю. Любой столбец содержит значения соответствующего критерия, достигаемые при оптимизации по всем критериям.
- значение i- го критерия при оптимизации по j- му критерию. Ясно, что диагональное элементы равны единице, а все прочие меньше единицы. Очевидно, что после нормировки наибольшее значение каждого критерия равно единице, а наименьшее нулю. Любой столбец содержит значения соответствующего критерия, достигаемые при оптимизации по всем критериям.
Таблица содержит ценную информацию, а именно область допустимых значений. Так, если значения каких-то двух столбцов близки для каждой из строк (кроме строк, которые содержат единицы в этих столбцах), то два соответствующих критерия сильно зависимы, так как изменения всех иных критериев (кроме этих двух) одинаково влияют на эти два критерия. Можно выявить также и противоречивые критерии, когда высокая оценка по одному сопровождается низкой оценкой по другому критерию. Такая информация полезна для ЛПР, анализирующего областью D допустимых значений.
2. По данным таблицы 4 вычисляются индексы критериев. Пусть 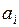 - среднее значение, вычисленное по всем элементам i- го столбца (кроме единицы). Тогда индекс i- го критерия
- среднее значение, вычисленное по всем элементам i- го столбца (кроме единицы). Тогда индекс i- го критерия 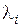 вычисляется из соотношений:
вычисляется из соотношений:
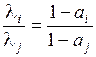 ,
, 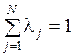 (3)
(3)
Индекс критериев имеет смысл коэффициента внимания, котороеследует уделять критерию при поиске решения.
Предположим, что все элементы i- го столбца в таблице 4 близки к единице.Тогда среднее значение тоже близко к единице, 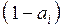 мало и соответствующий индекс мал. Действительно, если при оптимизации по другим критериям значение данного критерия близко к наилучшему, то ему вряд ли стоит уделять внимание. Наоборот, критерию, сильно зависящему от изменений других критериев (
мало и соответствующий индекс мал. Действительно, если при оптимизации по другим критериям значение данного критерия близко к наилучшему, то ему вряд ли стоит уделять внимание. Наоборот, критерию, сильно зависящему от изменений других критериев ( 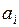 мало), должны соответствовать большие значения индекса. Индексы называют иногда техническими весами потому, что в отличие от весов
мало), должны соответствовать большие значения индекса. Индексы называют иногда техническими весами потому, что в отличие от весов 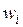 , они не назначаются ЛПР, а вычисляются.
, они не назначаются ЛПР, а вычисляются.
3. Производится глобальная оптимизация по комплексному критерию вида
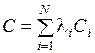 (4)
(4)
где 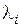 , определяют из (3). Решение, найденное в результате оптимизации, предъявляют ЛПР.
, определяют из (3). Решение, найденное в результате оптимизации, предъявляют ЛПР.
Фаза анализа:
1. ЛПР анализирует вектор значений критериев 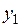 , найденный при оптимизации по критерию (4). Затем ему задается вопрос: все ли компоненты вектора
, найденный при оптимизации по критерию (4). Затем ему задается вопрос: все ли компоненты вектора 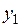 имеют удовлетворительные значения? Если да, то решение получено. Если нет, то ЛПР указывает один критерий с наименее удовлетворительным значением.
имеют удовлетворительные значения? Если да, то решение получено. Если нет, то ЛПР указывает один критерий с наименее удовлетворительным значением.
2. ЛПР просят назначить для критерия с наименее удовлетворительным значением пороговое значение 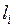 , при достижении которого можно признать этот критерий имеющим удовлетворительное значение:
, при достижении которого можно признать этот критерий имеющим удовлетворительное значение:
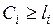 (5)
(5)
Условие (5) добавляется к совокупности линейных равенств и неравенств, определяющих область D допустимых значений переменных. Таким образом, возникнет новая область допустимых значений.
На этом фаза анализа заканчивается. Следующий шаг начинается с фазы расчетов при новой области допустимых значений и т.д. При достижении удовлетворительных для ЛПР значений по всем критериям ЧМП завершается.
17. Пример применения процедуры «STEM» для управления персоналом
Французской консультативной фирмой SEMA предложена методика анализа изменения состава персонала и продуктивности работы организации. Модель применялась для прогнозирования последствий различных вариантов управления кадрами организации. Тестировались разные стратегии приема на работу и повышения в должности через два, три и четыре года.
В качестве переменных модели рассматривалось количество сотрудников, назначенных на различные должности в определенные периоды времени. Применялись четыре критерия в виде линейные функции от переменных:
1. общая укомплектованность кадров - SA;
2. фактическая эффективность работы кадров - EF;
3. стоимость приема на работу дополнительных сотрудников - EB;
4. стоимость нехватки кадров по отношению к прогнозируемым потребностям - EC.
Модель учитывала следующие закономерности:
Ø эффективность работы сотрудника линейно зависит от отношения оценки его возможностей Q к оценке требований t, определяемых должностью сотрудника;
Ø удовлетворение сотрудника во время пребывания на определенной должности сначала возрастает до максимального значения, а затем со временем уменьшается до первоначального значения также в зависимости от отношения Q к t.
С математической точки зрения проблеме представляли собой задачу линейного программирования с четырьмя критериями качества, 350 переменными и 200 ограничениями. Отсутствовала априорная информация о сравнительной важности критериев.
Решение формировалось методом «STEM». На первом этапе анализа в области допустимых значений выполняли оптимизацию по каждому из критериев в отдельности. На втором этапе выполняли преобразование значений критериев к относительным величинам из интервала (0,1). Результаты вычислений представлены в таблице 5.
Из рассмотрения таблицы следуют следующие выводы:
Ø имеет место сильная зависимость критериев SA и EF;
Ø критериев EB и EC противоречат друг другу;
Ø критерии SA и EF противоречат критериям EB и EC.
Таблица 5.
Результаты поочередной оптимизации критериев
| Критерий | SA | EF | EB | EC |
| SA | 0,875 | 0,275 | 0,83 | |
| EF | 0,86 | 0,09 | 0,765 | |
| EB | 0,131 | 0,149 | 0,4 | |
| EC | 0,442 | 0,45 | 0,733 |
На третьем этапе по данным таблицы 5 вычисляли начальные индексы (технические веса) критериев. Пусть 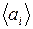 - среднее значение всех элементов по i- му столбцу (кроме единицы). Индексы критериев находили из условия
- среднее значение всех элементов по i- му столбцу (кроме единицы). Индексы критериев находили из условия
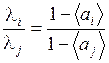 ,
, 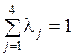 .
.
что позволило получить оценки технических весов
| Критерий | SA | EF | EB | EC |
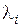
| 0,261 | 0,254 | 0,317 | 0,168 |
и, в свою очередь, найти в области допустимых решений вершину с наилучшими значениями по всем критериям.
На четвертом этапе выполнялась глобальная оптимизация по комплексному критерию вида (3), что позволило получить следующий результат:
SA = 0,965; EF = 0,85; EB = 0,45; EC = 0,675.
Для диалога с ЛПР предъявлялись:
Ø вектор 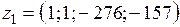 максимальных значений, достигаемых при максимизации по каждому из критериев по отдельности. Критерии EB и EC были представлены в единицах стоимости;
максимальных значений, достигаемых при максимизации по каждому из критериев по отдельности. Критерии EB и EC были представлены в единицах стоимости;
Ø вектор 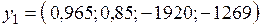 значений критериев, достигаемых в результате оптимизации по комплексному критерию (3) с приведенными выше индексами.
значений критериев, достигаемых в результате оптимизации по комплексному критерию (3) с приведенными выше индексами.
Перед ЛПР был поставлен вопрос: все ли компоненты вектора 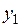 имеют удовлетворительные значения? При ответе на этот вопрос использовался вектор
имеют удовлетворительные значения? При ответе на этот вопрос использовался вектор 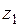 , компоненты которого представляли собой максимально возможные (недостижимые одновременно) значения компонентов вектора
, компоненты которого представляли собой максимально возможные (недостижимые одновременно) значения компонентов вектора 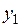 . Руководитель определил значение по критерию EB как наименее удовлетворительное и назначил нижний уровень по критерию EB = -1000.
. Руководитель определил значение по критерию EB как наименее удовлетворительное и назначил нижний уровень по критерию EB = -1000.
Далее были найдены максимально возможные значения трех остальных критериев при ограничениях, дополнительно накладываемых на критерий EB:
| Критерий | EB > -750 | EB > -1000 | EB > -1250 | EB > -1500 |
| SA | 0,67 | 0,78 | 0,84 | 0,9 |
| EF | 0,62 | 0,72 | 0,82 | 0,88 |
| EC | -731 | -157 | -57 | -157 |
В результате анализа этой таблицы руководитель выбрал вектор решений для ограничения ЕВ > -1500 как обеспечивающий приемлемый компромисс между повышением качества по критерию ЕВ и понижением качества по критериям SA и EF.
Для новой области допустимых решений (ЕВ > -1500) приведенным выше способом были подсчитаны новые значения индексов для трех критериев:
| Критерий | SA | EF | EC |
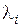
| 0,885 | 0,775 | 0,91 |
На второй итерации уточнения решения в результате диалога с ЛПР проводилась глобальная оптимизация по комплексному критерию с индексами. Полученные решения
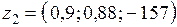 и
и 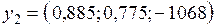 ,
,
достигаемых в новой области допустимых значений переменных, было предъявлено ЛПР во время третьего диалога ним. Руководитель определил значение по критерию ЕС как наименее удовлетворительное и назначил нижний уровень по критерию ЕС = -600. Затем были определены максимально возможные значения двух критериев при ряде ограничений, накладываемых на критерий ЕС:
| Критерий | EC > -800 | EC > -600 | EC > -400 |
| SA | 0,85 | 0,8 | 0,73 |
| EF | 0,8 | 0,75 | 0,68 |
Руководитель выбрал вектор решений для ограничения EC > -800 как обеспечивающий приемлемый компромисс между повышением качества по критерию ЕС и понижением качества по критериям SA и EF. Учитывая наличие сильной зависимости критериям SA и EF, он выбрал решение, соответствующее максимуму EF, как окончательное решение проблемы:
SA = 0,76; EF = 0,8; EB = -1500; EC = 55 - 800.
Блок-схема метода «STEM» приведена на рисунке 20.
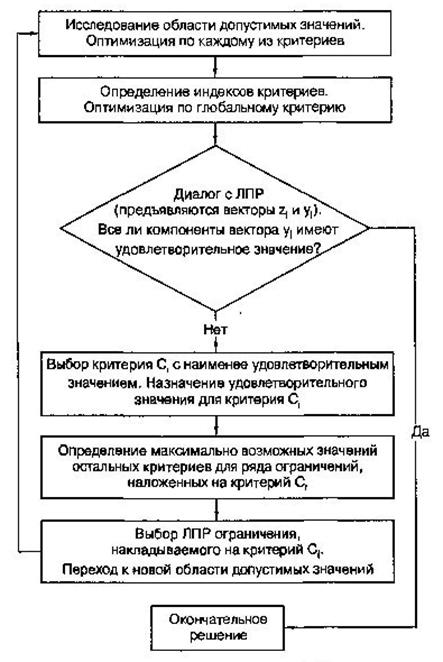
Рисунок 20. Блок схема метода «STEM».
Выводы
1. Предшественниками методов принятия решений во многих случаях являются методы исследования операций. С помощью этих методов:
а) разрабатывают модели, описывающие объективную реальность;
б) определяют единственный критерий оптимальности решения;
в) рассчитывают оптимальное решение.
2. Существенное отличие проблем принятия решений от проблем исследования операций состоит в наличии многих критериев оценки качества решения Компромисс между критериями может быть найден только на основе предпочтений ЛПР.
3. Существует особый класс задач принятия решений, в которых модели имеют объективный характер (как в задачах исследования операций), но качество решений оценивается по многим критериям.
Эти задачи называют многокритериальными задачами с объективными моделями. Они находятся на границе между исследованием операций и принятием решений. Одним из первых многокритериальных методов является метод стоимость – эффективность. Он включает в себя два этапа.
1. построение моделей стоимости и эффективности;
2. синтез оценок стоимости и эффективности.
На втором этапе применяют подходы:
• оптимизации по одному критерию при заданном ограничении по второму;
• построение множества Э – П.
4. Средством решения многокритериальных задач с объективными моделями являются человеко-машинные процедуры (ЧМП). ЧМП представляют собой циклический процесс взаимодействия ЛПР и компьютером. Каждый шаг ЧМП состоит из фазы анализа, выполняемого ЛПР и фазы расчетов, выполняемого компьютером.
5. Можно выделить три группы ЧМП:
1) прямые, основанные на выборе коэффициентов важности критериев;
2) ЧМП сравнения векторов;
3) ЧМП поиска удовлетворительных значений критериев.
Одной из первых ЧМП является STEM, основанная на идее последовательного наложения ограничений на критерии.
Дата добавления: 2019-10-16; просмотров: 1188;
