Признаки сходимости для рядов с положительными членами.
Как и в случае несобственных интегралов, важнейшим элементом теории числовых рядов является следующий: надо, не вычисляя ряда, ответить на вопрос, сходится он или нет. В конце концов, если он сходится, то его можно вычислить численно на ЭВМ, а вот если он расходится - попытки сосчитать его численно ни к чему хорошему не приведут.
В данном разделе будут
Рассмотрены признаки сходимости рядов с положительными членами. Итак, пусть даны два ряда 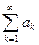 и
и 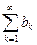 и выполнено условие
и выполнено условие 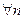
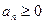 и
и 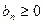 .
.
Теорема 1. Для сходимости ряда 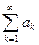 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы
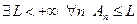 .
.
Доказательство. Имеем: 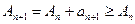 и поэтому с ростом п
и поэтому с ростом п 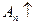 . По теореме о существовании предела монотонно возрастающей последовательности, для существования конечного
. По теореме о существовании предела монотонно возрастающей последовательности, для существования конечного 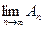 необходимо и достаточно,
необходимо и достаточно,
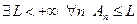 . <
. <
Теорема 2. Пусть даны два ряда 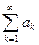 (ряд А) и
(ряд А) и 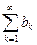 (ряд В) с положительными членами и выполнено условие
(ряд В) с положительными членами и выполнено условие 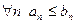 . Тогда из сходимости ряда В следует сходимость ряда А, а из расходимости ряда А - расходимость ряда В.
. Тогда из сходимости ряда В следует сходимость ряда А, а из расходимости ряда А - расходимость ряда В.
Доказательство.
1. Пусть ряд В сходится Þ 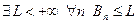 . Но
. Но 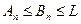 Þ ряд А сходится.
Þ ряд А сходится.
2. Пусть ряд А расходится. Так как в этом случае 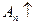 , то это означает, что
, то это означает, что 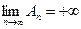 . Но так как
. Но так как 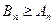 , то
, то 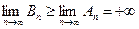 и поэтому
и поэтому 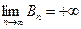 и ряд В расходится. <
и ряд В расходится. <
Замечание. Так как Отбрасывание или изменение конечногочисла членов ряда не изменяет его сходимости, то условие 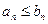 может выполняться лишь
может выполняться лишь 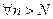 .
.
Дата добавления: 2019-07-26; просмотров: 148;
