Простейшие свойства сходящихся рядов
Числовые ряды. Определения
Пусть дана последовательность вещественных чисел 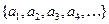 . Образуем новую последовательность по правилу
. Образуем новую последовательность по правилу
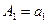 ;
; 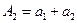 ;
; 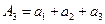 ; … ;
; … ; 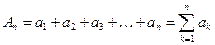 .
.
Эти величины называются частными суммамичислового ряда, а слагаемое 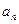 называют общим членомряда.
называют общим членомряда.
Рассмотрим теперь 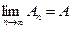 . Он называется числовым рядоми обозначается символом
. Он называется числовым рядоми обозначается символом
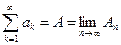 .
.
Если этот предел существует и конечен, то говорят, что числовой ряд сходится, а само значение предела, то есть величину А, называют суммойчислового ряда. Если этот предел не существует или бесконечен, то говорят, что числовой ряд расходится(так как в данной главе других рядов не будет, то слово «числовой» мы будем опускать).
Обратите внимание на одну деталь: индекс суммирования в знаке бесконечной суммы может быть любым, то есть
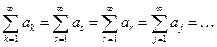 ,
,
от этого ничего не меняется. Как говорят, индекс суммирования является немым индексом,то есть он может быть обозначен любой буквой.
Величина
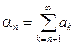
называется остатком ряда после n-го слагаемого.Его можно записать и так:
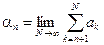 .
.
Простейшие свойства сходящихся рядов
1. Если ряд сходится, то сходится любой из его остатков. Наоборот, из сходимости остатка вытекает сходимость исходного ряда.
Доказательство.
Имеем:
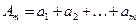
- частная сумма исходного ряда и
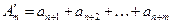
- частная сумма остатка ряда после п-го слагаемого. Очевидно, что между этими величинами имеет место соотношение
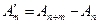
Если ряд сходится Þ 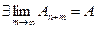 Þ
Þ 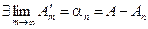 Þ остаток ряда после п-го слагаемого.
Þ остаток ряда после п-го слагаемого.
Далее, 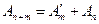 , и поэтому
, и поэтому
Если сходится остаток ряда после п-го слагаемого Þ 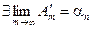 Þ
Þ 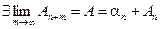 Þ исходный ряд сходится.
Þ исходный ряд сходится.
Обратите внимание на важное для дальнейшего соотношение 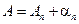 .
.
Следствие. Отбрасывание или изменение конечногочисла членов ряда не изменяет его сходимости.
2. Если ряд 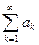 сходится, то
сходится, то 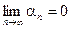 .
.
Действительно, из соотношения 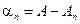 получаем
получаем
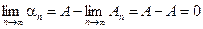 .
.
3. Если ряд 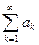 сходится, то его общий член стремится к нулю, то есть
сходится, то его общий член стремится к нулю, то есть 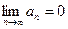 .
.
Действительно, из определения частных сумм легко видеть, что 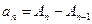 . Поэтому
. Поэтому
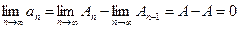
Следствие. (важно!)Признак расходимостиряда.
Если общий член ряда не стремится к нулю, то ряд расходится.
4. Если ряд 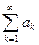 сходится, то ряд
сходится, то ряд 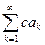 тоже сходится и верно соотношение
тоже сходится и верно соотношение
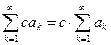 . Действительно, для частных сумм наших рядов имеем
. Действительно, для частных сумм наших рядов имеем
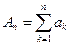 ;
; 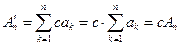
Делая предельный переход 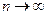 , получаем
, получаем
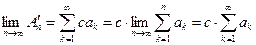 .
.
5. Если ряды 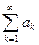 и
и 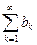 сходятся, то ряд
сходятся, то ряд 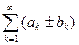 тоже сходится и верно соотношение
тоже сходится и верно соотношение
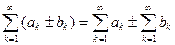 .
.
Действительно, из определения частных сумм рядов получаем
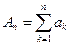 ;
; 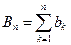 ;
; 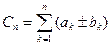 .
.
Отсюда видно, что между частными суммами рядов верно соотношение
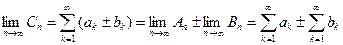 .
.
Дата добавления: 2019-07-26; просмотров: 259;
