Понятие электронного облака. Его физический смысл.
Общий вид волновых функций достаточно сложен.
Рассмотрим для примера волновую функцию основного состояния электрона– 1s-состояние, т.е. состояния с минимальной энергией: n = 1, l = 0, m = 0.
Кратность вырождения n2 = 1, т. е. состояние невырожденное. Так как l = 0, то М = 0, Мz = 0.
Функция Y, представляющая собой собственную функцию оператора квадрата момента импульса для s-состояния (с нулевым моментом импульса) будет постоянной. Это соответствует тому, что движение электрона не зависит от углов θ и φ и будет только радиальным, а пси-функция 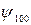 ( а также все пси-функции вида
( а также все пси-функции вида 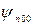 ) зависит только от r и будет сферически симметричной.
) зависит только от r и будет сферически симметричной.
Решение уравнения Шредингера для s-состояния дает следующий вид пси-функции
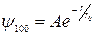 ,
,
где r0 – радиус первой боровской орбиты, A – нормирующая константа.
Так как от понятия траектории пришлось отказаться, то ввели понятие «электронного облака», плотность распределения которого в каждой точке пропорциональна плотности вероятности местонахождения электрона в этой точке.
Плотность вероятности обнаружить электрон на расстоянии r будет определяться с учетом того, что элемент объема в сферической системе координат
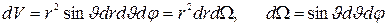 ,
,
где 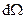 - элемент телесного угла. Проинтегрировав это выражение по полному телесному углу 4π, найдем вероятность того, что электрон окажется в тонком шаровом слое между r и r + dr
- элемент телесного угла. Проинтегрировав это выражение по полному телесному углу 4π, найдем вероятность того, что электрон окажется в тонком шаровом слое между r и r + dr
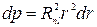
Плотность вероятности нахождения электрона на расстоянии r от ядра определяется величиной
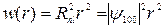 .
.
Графически распределение плотности вероятности выглядит, например для состояния 1s следующим образом (рис.4).
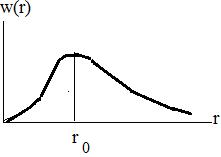
Рис.4
Плотность вероятности w(r) обращается в нуль при r = 0 и асимптотически стремиться к нулю при 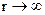 . Таким образом, имеется определенная вероятность найти электрон на любом расстоянии от ядра. Мы можем определить расстояние, на котором эта вероятность будет максимальна. Полученный результат покажет, что максимум вероятности будет соответствовать расстоянию от ядра, совпадающему с величиной радиуса первой боровской орбиты r0. Так как состояние 1s характеризуется сферической симметрией, то распределение вероятности представляет собой сферическое облако, а не плоский образ, соответствующий боровской орбите.
. Таким образом, имеется определенная вероятность найти электрон на любом расстоянии от ядра. Мы можем определить расстояние, на котором эта вероятность будет максимальна. Полученный результат покажет, что максимум вероятности будет соответствовать расстоянию от ядра, совпадающему с величиной радиуса первой боровской орбиты r0. Так как состояние 1s характеризуется сферической симметрией, то распределение вероятности представляет собой сферическое облако, а не плоский образ, соответствующий боровской орбите.
Пример для состояния 2s: n = 2, l = 0, m = 0 (рис.5).

Рис.5
Пространственное квантование момента импульса имеет следующий вид (рис.6)
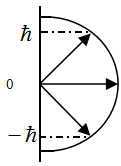
Рис.6
Угловое распределение плотности вероятности нахождения электрона в атоме водорода определяется видом угловой функции 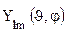
1) в s-состоянии (l = 0) 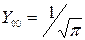
2) в p –состоянии (l = 1, m = -1, 0, +1)
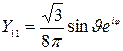
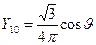
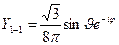 (Рис.7)
(Рис.7)

Рис.7
Для получения пространственного образа надо представить себе тело вращения, возникающее путем вращения избраженных фигур вокруг соответствующих осей.
Вопросы для самоконтроля:
1. Запишите уравнение Шредингера, которому удовлетворяет состояние электрона в атоме водорода.
2. Что характеризует квантовые числа: главное n, орбитальное l и магнитное m? Какие значения они могут принимать?
3. Каковы возможные значения l и m, для главного квантового числа n=3?
4. Сколько различных состояний соответствует n=2?
5. Чему равна плотность вероятности обнаружения электрона в основном состоянии атома водорода?
6. Атом водорода может иметь одно и тоже значение энергии находясь в различных состояниях? Как они называются?
7. Каковы правила квантования орбитального и собственного моментов импульса электронов? Их проекций на направления внешнего магнитного поля?
8. Что представляет из себя электронное облако? Каков его смысл?
Лекция 8.
Дата добавления: 2019-07-26; просмотров: 634;
