АЛГОРИТМИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ И АДАПТАЦИИ

В некоторых задачах оптимизации объектов требуется определить либо вектор оптимальных управлений U^o (см. §3.2), либо вектор пара­метров оптимальной настройки регулятора К° (см. §3.10). При этом критерий качества, характеризующий оптимальный режим работы объекта, представляет собой функцию многих переменных J(С), где вектором 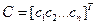обозначены векторы искомых управлений или параметров.

В задачах адаптивного управления также требуется определить либо вектор управлений U^o (T_i), либо вектор параметров самонастрой­ки регулятора 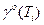на интервалах .

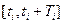К функционалам, зависящим от вектора параметров, можно сводить функционалы, зависящие от функций, поэтому алгоритмические ме­тоды оптимизации и адаптации рассмотрим при решении задач оптими­зации, когда критерии качества для детерминированных и вероятно­стных задач имеют вид [23]

J (С) = Q( X, С); (3.229)

J (С) = М_х {Q(X, С)}, (3.230)

где X – вектор координат состояния; М_х – символ математического ожидания по множеству реализаций вектора X.

Для эргодических стационарных процессов вместо (3.230) можно использовать критерий качества, основанный на усреднении по вре­мени:

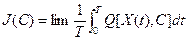. (3.231)о

Если функционал J(С) допускает дифференцирование по вектору С, то он достигает экстремума при таких значениях вектора С°, для ко­торых

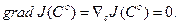(3.232)

Решение задачи оптимизации аналитическими методами дает ана­литические выражения для искомых векторов управлений или парамет­ров. Однако эти методы пригодны для решения относительно простых задач.

Для решения уравнений (3.232) и определения вектора 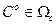используют различные итеративные методы. Физический смысл их со­стоит в замене алгебраических уравнений (3.232) относительно компо­нент вектора С разностными или дифференциальными уравнениями относительно этого же вектора С. Решение разностных или дифферен­циальных уравнений определяет искомый вектор С°, но не дает яв­ного решения уравнений (3.232); оно характеризует алгоритмы, оп­ределяющие последовательность действий (операций), выполнение которых приводит к искомому решению. Поэтому итеративные методы, используемые в задачах оптимизации и адаптации, называют алго­ритмическими методами [23].

Регулярные алгоритмы в задачах на безусловный экстремум.Основная идея решения уравнений (3.232) итеративными методами со­стоит в следующем. Уравнение (3.232) записывается в виде

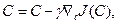(3.233)

где 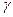– некоторый скаляр.

На основании (3.233) вектор С°, соответствующий минимуму J (С), ищется с помощью последовательных приближений или итераций вида

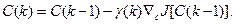(3.234)

Значение 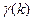определяет величину очередного шага по градиенту (см. § 3.2) и в общем случае зависит от номера шага k и векторов С (m), где т = k – 1, k – 2, ..., 0. Если выполняются условия сходимости, то для любого начального вектора С (0) получим

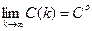(3.235)

Начальное значение С(0) однозначно предопределяет последова­тельности С(k) для детерминированных задач [см. критерий (3.229)], поэтому итеративные методы, определяемые рекуррентным соотно­шением (3.234), называют регулярными. Формы регулярных итера­тивных методов различны в зависимости от .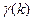

Беспоисковые алгоритмы. Если рекуррентное со­отношение (3.234) используют для определения оптимального вектора С° в задачах оптимизации, то его называют – алгоритмом оптимиза­ции в рекуррентной форме. Введем первую разность вектора С

DС(k - 1) = С(k) - С(k - 4),

после чего вместо (3.234) запишем разностное уравнение

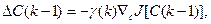(3.236)

которое называют алгоритмом оптимизации в разностной форме. Просуммируем обе части уравнения (3.236) от 0 до k, тогда получим уравнение

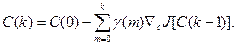(3.237)

называемое алгоритмом оптимизации в суммарной форме.

Для увеличения скорости сходимости алгоритмов оптимизации вме­сто скаляра 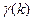вводят матрицу 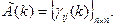При этом урав­нение (3.236) принимает вид

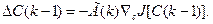(3.238)

Величины шагов по различным компонентам вектора С различны и зависят друг от друга.

Алгоритмы оптимизации (3.238) различают в зависимости от формы матрицы Г(k):

если Г(k)= Г = const, то получаем алгоритм оптимизации с по­стоянным шагом, или стационарный алгоритм;

если Г(k)зависит от k, то получаем алгоритм оптимизации с пере­менным шагом, или нестационарный алгоритм;

если Г(k + k₀)= Г(k), то матрица Г(k)периодична и алгоритм оптимизации является циклическим.

В общем случае Г(k)может зависеть от вектора С(т), где т = k – 1, k – 2, ..., 0, тогда алгоритм оптимизации (3.238) имеет «нелинейный» шаг. В зависимости от формы матрицы Г(k,С) разли­чают алгоритмы с нелинейным шагом:

если Г(k, С) = Ig(k, С), где I – единичная матрица, g(k, С) – скаляр, то алгоритм оптимизации называют градиентным;

если Г(k, С) = g(k, С)–скаляр, выбираемый на каждом шаге из условия минимума функции

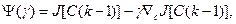(3.239)

то алгоритм оптимизации называют алгоритмом наискорейшего спуска.

Дискретному алгоритму в разностной форме (3.238) соответствует дискретная замкнутая система, блок-схема которой представлена на рис. 3.9, где МУ – матричный усилитель, определяемый выражением Г(k); ДИ – дискретный интегратор (дигратор); НП – нелинейный преобразователь, определяющий градиент критерия качества 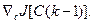В соответствии с уравнением первой разности запишем 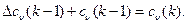Следовательно, структурная схе­ма дигратора будет представлять собой элемент запаздывания (ЭЗ)с положительной обратной связью (рис. 3.10). Для улучшения сходи­мости алгоритмов оптимизации, обеспечения их устойчивости и умень­шения времени определения С в соответствии с указанной блок-схе­мой можно применить методы коррекции и оптимизации импульсных систем.

Алгоритмы оптимизации (3.234), (3.236), (3.237) и (3.238) относятся к одношаговым алгоритмам и являются алгоритмами первого порядка, так как представляются в виде векторного разностного уравнения первого порядка.

Если функционал J (С) имеет несколько экстремумов, то одношаговые алгоритмы позволяют определить только локальные экстремумы. Поэтому необходимо выполнить расчеты при различных начальных век­торах С_i (0) и полученные J (C_i°) сравнить, чтобы определить вектор С° , соответствующий глобальному (абсолютному) экстремуму.

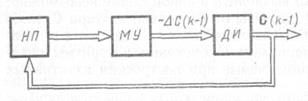Рис. 3.9

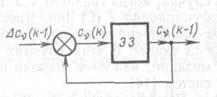Рис. 3.10

Для нахождения глобального экстремума можно применить мно­гошаговые алгоритмы, например алгоритм вида [23]

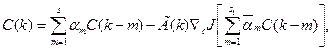(3.240)

где 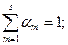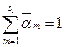, который при s = s₁ = 1 вырождается в одно шаговый алгоритм (3.238).

Выбирая а_т (k), a_m (k) и Г (/г), можно добиться того, чтобы алгоритм (3.240) был малочувствительным к локальным экстремумам. Приме­нение многошагового алгоритма (3.240) в задачах оптимизации, когда J (С) имеет единственный экстремум, позволяет повысить помехоустой­чивость и ускорить сходимость при определении С⁰.

Дискретным алгоритмам оптимизации можно поставить в соответ­ствие непрерывные алгоритмы. Если, например, в (3.238) заменить k на t, а разности на производные, то при предельном переходе получим непрырывный алгоритм оптимизации первого порядка в виде вектор­ного дифференциального уравнения первого порядка относительно вектора С (t):

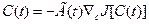. (3.241)

Непрерывному алгоритму (3.241) соответствует непрерывная зам­кнутая система; ее условная схема аналогична схеме, изображенной на рис. 3.9, в которой следует заменить Г (k)на Г (t)и дигратор на непрерывный матричный интегратор. Непрерывный алгоритм (3.241) можно реализовать на АВМ.

Для определения глобального экстремума и улучшения процессово пределения С° в случае единственного экстремума функционала J (С) можно применить непрерывные алгоритмы высшего порядка в виде векторного дифференциального уравнения s-гo порядка относительно вектора С (t):1

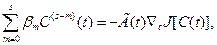(3.242)

где 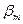–коэффициенты, которые выбирают так, чтобы обеспечить же­лаемое качество процесса определения С^o. Алгоритмы высшего порядка (3.242) могут быть реализованы на АВМ.

Поисковые алгоритмы. На практике встречаются случаи, когда градиент 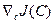вычислить в явной форме невозможно: функционал J (С) либо имеет разрывы относительно вектора С, либо недиффиренцируем по С, либо его зависимость от С выражена в неявной форме. В этих случаях используют поисковые алгоритмы оптимизации, наиболее широко применяемые при построении адаптивныхсистем [14].

При поисковых алгоритмах измеряют функционал или какие-либо величины, косвенно оценивающие градиент 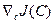. Введем векторы, компонентами которых являются значения функционала при измененных значениях вектора С (k)на величину «пробного шага» g:

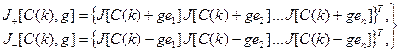(3.243)

где 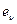– базисные векторы: е₁ = [1 0 ... 0]^T; е₂ = [0 1 0... 0]^T; е_n = [00 ...0 1]^T.

Введем также вектор, компонентами которого являются значения функционала при неизменных значениях вектора С (k):

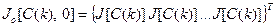. (3.244)

Тогда градиент можно оценить по формулам при поиске с односто­ронним «пробным шагом»

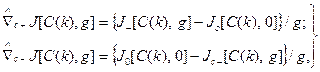(3.245)

с двусторонними «пробными шагами»

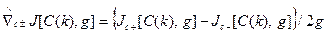, (3.246)

где 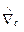– символ оценки градиента по вектору С.

Поисковый алгоритм оптимизации на основании уравнения (3.238) с учетом (3.246) запишется как

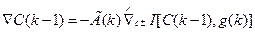(3.247)

Алгоритму (3.247) соответствует дискретная система, схема которой отличается от схемы, изображенной на рис. 3.9, наличием генератора поисковых сигналов, формирующих g(k), и устройства оценки градиента. Если шаг g (k)однозначно определяется значением функцио­нала или его градиента, то поиск является регулярным. Если шаг вы­бирается в произвольном направлении и не зависит от абсолютного значения функционала или его градиента, то поиск является случайным [14].

Поисковые алгоритмы широко используют в адаптивных системах, особенно в экстремальных. Методы случайного поиска особенно эффек­тивны для многомерных объектов с многоэкстремальными характе­ристиками [14].

Регулярные алгоритмы в задачах на условный экстремум. Усло­виями некоторых задач оптимизации, кроме функционала критерия качества, являются функциональные ограничения в виде уравнений объекта, связывающих координаты выхода, состояния и управлений. Кроме того, в ряде случаев координаты состояния, выхода и управ­лений ограничены по величине и принадлежат некоторым множествам (см. § 1.3). Как было указано в §3.2, такие задачи называют задачами оптимизации на условный экстремум.

Если указанные ограничения представлены в виде равенств g(С) = 0, то в соответствии с методом множителей Лагранжа записывается функционал

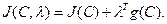(3.248)

В этом случае условием минимума 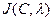являются равенства

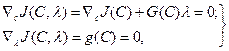(3.249)

где 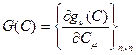–матрица размерности 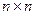; u = 1, 2, … , n; m = 1, 2, ..., п.

Алгоритмы оптимизации в задачах на условный экстремум, определяющие С^o и l°, на основании (3.249) запишутся как [23]

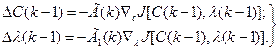(3.250)

Алгоритмам (3.250) можно поставить в соответствие непрерывные алгоритмы, записать многошаговые алгоритмы типа (3.240) и поисковые алгоритмы типа (3.247).

Алгоритмам (3.250) соответствует дискретная замкнутая система, схема которой в отличие от схемы, изображенной на рис. 3.9, будет иметь дополнительный контур для определения вектора l(k – 1), необходимого для вычисления .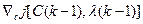

Если ограничения представлены в виде неравенств g(С) ≤ 0, то условия минимума (3.249) записывают в соответствии с теоремой Куна – Таккера (см. § 3.2), после чего составляют алгоритмы оптимизации.

Вероятностные алгоритмы. Для вероятностных задач оптимизации критерий качества является статистической оценкой функционала Q(X, С) в виде его среднего значения по множеству реализаций [см. (3.230)] или по времени [см. (3.231)]. Уравнения ограничений для таких объектов также представляют средними значениями

h (С) = М_х {g (X, С)} ≤ 0. (3.251)

Задача оптимизации в этом случае состоит в том, чтобы подобрать такой оптимальный вектор С⁰, при котором среднее значение функционала имеет минимум.

Для определения вектора С^o, доставляющего экстремум функционалу (3.230), который в явном виде неизвестен, регулярные итеративные методы непригодны. Такие задачи решают вероятностными итеративными методами, основную идею которых можно пояснить следующим образом.

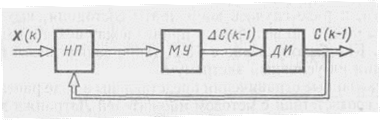
Рис. 3.11

Условие оптимальности (3.232) для стохастических объектов записывается уравнением

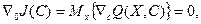(3.252)

в котором неизвестен градиент 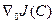, а известны лишь реализации .

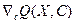Если выбрать надлежащим образом матрицу Г(k), то вероятностный алгоритм оптимизации можно представить подобно регулярным алгоритмам в рекуррентной, разностной и суммарной формах соответственно:

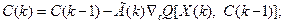(3.253)

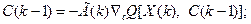(3.254)

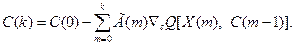(3.255)

Вероятностные алгоритмы называют алгоритмами стохастической аппроксимации.

Существенным отличием вероятностных алгоритмов от регулярных является то, что при С = С^o

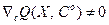, (3.256)

в то время как для регулярных алгоритмов 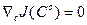. Из-за этой особенности матрицу Г(k)необходимо выбирать так, чтобы обеспечить сходимость вероятностных алгоритмов. В простейших вероятностных алгоритмах ее выбирают в виде диагональной

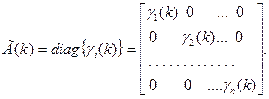(3.257)

В частных случаях принимают одинаковые компоненты: .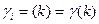

Вероятностным алгоритмам оптимизации можно поставить в соответствие непрерывный алгоритм в виде стохастического векторного дифференциального уравнения первого порядка

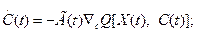(3.258)

Алгоритму (3.254) соответствует дискретная замкнутая система, блок-схема которой представлена на рис. 3.11.

Аналогично рассмотренным способам формирования многошаговых и поисковых регулярных алгоритмов оптимизации можно составить многошаговые и поисковые вероятностные алгоритмы оптимизации. При этом следует учитывать ограничения типа (3.251) и составлять соответствующие вероятностные алгоритмы в стохастических задачах оптимизации на условный экстремум [23]. Регулярные и вероятностные алгоритмы оптимизации используют для поиска экстремума в экстремальных системах (см. гл. 4), для определения параметров настройки регуляторов, а также для идентификации объектов в самонастраивающихся системах (см. гл. 7).