МЕТОДЫ РАСЧЕТА ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ПАРАМЕТРОВ
В инженерной практике часто ставится задача определения оптимальных значений параметров системы, структура и дифференциальные уравнения которой заданы. Такая задача обычно решается при расчете параметров оптимальной настройки регуляторов. При этом могут быть использованы уравнения Эйлера–Лагранжа (или Эйлера-Пуассона), уравнения Риккати, а также частотные методы и др.
Математически задачу определения параметров оптимальной настройки системы можно сформулировать следующим образом: заданы дифференциальные уравнения состояния системы
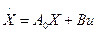 ;
; 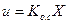 , (3.186)
, (3.186)
где 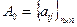 ;
; 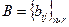 ;
; 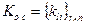 – матрица, элементы которой зависят от искомых параметров настройки системы (
– матрица, элементы которой зависят от искомых параметров настройки системы ( 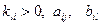 – коэффициенты уравнения объекта); X, u– векторы координат состояния и управлений;
– коэффициенты уравнения объекта); X, u– векторы координат состояния и управлений;
требуется определить оптимальные значения параметров системы из условия экстремума выбранного критерия качества.
В ряде практических задач коэффициенты 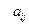 и
и 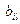 заданы и требуется определить коэффициенты
заданы и требуется определить коэффициенты 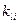 .
.
Если рассматривается критерий качества в виде интеграла с квадратичной подинтегральной функцией 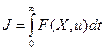 , то для определения искомых
, то для определения искомых 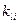 можно использовать уравнения вариационной задачи или уравнение Риккати. В тех случаях, когда рассматривается критерий качества в виде функции нескольких переменных (представляющих собой искомые параметры):
можно использовать уравнения вариационной задачи или уравнение Риккати. В тех случаях, когда рассматривается критерий качества в виде функции нескольких переменных (представляющих собой искомые параметры): 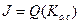 , для определения
, для определения 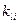 можно использовать методы поиска экстремума функции нескольких переменных и частотные методы.
можно использовать методы поиска экстремума функции нескольких переменных и частотные методы.
Расчет по уравнениям вариационной задачи.Известно, что для линейных одномерных объектов, динамика которых описывается линейным дифференциальным уравнением вида
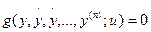 (3.187)
(3.187)
при квадратичном функционале критерия качества
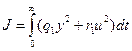 (3.188)
(3.188)
оптимальное управление, доставляющее минимум интегралу (3.188), является линейной функцией координат состояния [7], поэтому
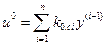 3.189)
3.189)
где 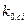 – коэффициенты обратных связей регулятора.
– коэффициенты обратных связей регулятора.
Если равенство (3.189) подставить в (3.187), то получим уравнение объекта, выраженное через координаты объекта и параметры регулятора 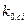 :
:
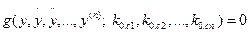 . (3.190)
. (3.190)
На основании (3.190) запишем характеристический полином системы F (р), и найдем сопряженный полином F (-р) после чего составим уравнение
F° (р) = F(p)F(-р). (3.191)
На основании (3.187) и (3.188) запишем функцию Лагранжа
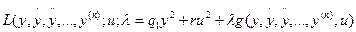 (3.191)
(3.191)
и уравнения вариационной задачи: уравнения Эйлера – Пуассона типа (3.61) для у и и уравнения (3.187). Из уравнений вариационной задачи получим уравнение
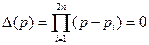 , (3.193)
, (3.193)
где П – знак произведения, подобное уравнению (3.191).
Приравнивая коэффициенты при одинаковых степенях р в уравнениях для F°(p) и 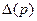 , получим алгебраические уравнения относительно неизвестных коэффициентов
, получим алгебраические уравнения относительно неизвестных коэффициентов 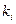 . Решение их позволяет найти искомые оптимальные параметры регулятора
. Решение их позволяет найти искомые оптимальные параметры регулятора 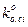 .
.
Расчет по уравнениям Риккати.Матрицу оптимальных параметров регулятора 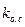 . с можно определить по заданным уравнениям состояния (3.186) с использованием матричного уравнения Риккати, основываясь на методе принципа максимума. Для линейных объектов уравнение (3.114) можно записать в виде (3.186), а минимизируемый квадратичный функционал в общем случае представить в виде
. с можно определить по заданным уравнениям состояния (3.186) с использованием матричного уравнения Риккати, основываясь на методе принципа максимума. Для линейных объектов уравнение (3.114) можно записать в виде (3.186), а минимизируемый квадратичный функционал в общем случае представить в виде
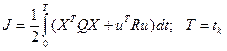 (3.194)о
(3.194)о
где 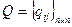 и
и 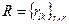 – матрицы, элементы которых
– матрицы, элементы которых 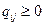 и
и 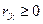 .
.
Известно, что вектор координат оптимальных управлений, доставляющих минимум интегралу (3.194), является линейной функцией координат состояния [см. (3.186)].
Функция Гамильтона, определяемая выражением (3.121), в данном случае при 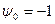 будет иметь вид
будет иметь вид
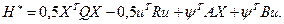 (3.195)
(3.195)
При оптимальном управлении
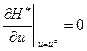 ,
,
или
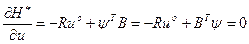 ,
,
откуда оптимальное управление
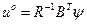 . (3.196)
. (3.196)
Управление (3.196) обеспечивает максимум гамильтониана (3.195), так как при положительно определенной матрице R
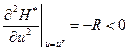 ,
,
Используя (3.195) и (3.196), запишем канонические уравнения:
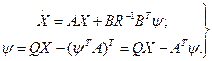 (3.197)
(3.197)
Для определения оптимального управления (3.196) необходимо из уравнений (3.197) найти вектор вспомогательных функций W (см. § 3.6).
Однако в данном случае можно не производить интегрирование уравнений (3.197), а использовать уравнение Риккати, что позволяет упростить решение задачи.
Рассмотрим способ получения уравнения Риккати. В общем случае можно записать уравнение
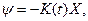 (3.198)
(3.198)
дифференцируя которое, найдем
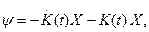 (3.199)
(3.199)
где 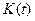 – матрица неизвестных коэффициентов размерности (пхп):
– матрица неизвестных коэффициентов размерности (пхп):
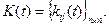
Подставив (3.198) в уравнения системы (3.197), получим:
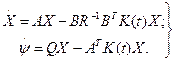 (3.200)
(3.200)
Если подставить в (3.199) вместо 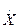 первое уравнение системы (3.200), то запишем
первое уравнение системы (3.200), то запишем
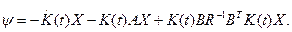 (3.201)
(3.201)
Приравнивая правые части уравнения (3.201) и второго уравнения (3.200), получим матричное дифференциальное уравнение
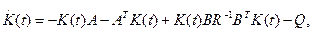 (3.202)
(3.202)
называемое уравнением Риккати. Решение уравнения (3.202) определяет матрицу 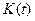 , подставляя которую в (3. 198) и учитывая (3.196), получим выражение для оптимального управления
, подставляя которую в (3. 198) и учитывая (3.196), получим выражение для оптимального управления
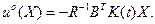 (3.203)
(3.203)
Для полностью управляемых объектов с постоянными во времени параметрами при 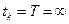 [см. (3.194)]
[см. (3.194)] 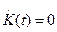 и
и 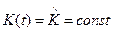 , поэтому оптимальное управление принимает форму
, поэтому оптимальное управление принимает форму
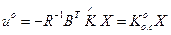 , (3.204)
, (3.204)
откуда
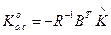 , (3.205)
, (3.205)
где 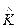 – положительно определенная симметричная матрица размерности (пxп), состоящая из постоянных коэффициентов
– положительно определенная симметричная матрица размерности (пxп), состоящая из постоянных коэффициентов 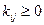 (при
(при 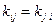 ), определяемая уравнением (3.202) с учетом
), определяемая уравнением (3.202) с учетом 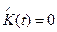 и
и 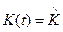 :
:
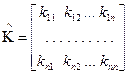 (3.206)
(3.206)
Оптимальное управление (3.204) минимизирует квадратичный функционал (3.194) для объектов с постоянными параметрами и 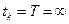 . Таким образом, для определения оптимальных параметров регулятора необходимо найти матрицу
. Таким образом, для определения оптимальных параметров регулятора необходимо найти матрицу 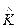 и подставить в (3.205). Для объектов с переменными параметрами, а также с постоянными параметрами при конечной величине
и подставить в (3.205). Для объектов с переменными параметрами, а также с постоянными параметрами при конечной величине 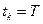 необходимо определять матрицу К(t). Основная трудность решения такой задачи состоит в том, что уравнение (3.202) является нелинейным дифференциальным матричным уравнением, для интегрирования которого требуется применение вычислительных машин. В этом случае регулятор будет иметь переменные параметры, т. е.
необходимо определять матрицу К(t). Основная трудность решения такой задачи состоит в том, что уравнение (3.202) является нелинейным дифференциальным матричным уравнением, для интегрирования которого требуется применение вычислительных машин. В этом случае регулятор будет иметь переменные параметры, т. е. 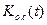 .
.
| <== предыдущая лекция | | | следующая лекция ==> |
| б) пластинчатые насосы | | | ОСОБЕННОСТИ ПРИМЕНЕНИЯ ТИПОВЫХ МЕТОДОВ СИНТЕЗА ОПТИМАЛЬНЫХ УПРАВЛЕНИЙ В ЗАДАЧАХ ВЕКТОРНОЙ ОПТИМИЗАЦИИ ОБЪЕКТОВ |
Дата добавления: 2019-07-26; просмотров: 450;
