Независимые множества
Множество вершин гиперграфа называется независимым, если оно не содержит ребер. Пустое множество вершин по определению независимо. Как и в случае графов, наибольшее по мощности независимое множество вершин гиперграфа Н называется наибольшим, а число вершив вэтом множестве называется числом независимости гиперграфа Н и обозначается через αо(Н). Через ГН обозначается множество, элементами которого служат все независимые множества вершин гиперграфа Н.
Очевидно, что изучая независимые множества вершин гиперграфе, естественно рассматривать гиперграфы без кратных ребер. Опишем, как каждому такому гиперграфу поставить в соответствие монотонную булеву функцию. Пусть Н — гиперграф, VH =(1,2, ..., п), xv=( х1,х2, ..., хп) — характеристический вектор произвольного подмножества U € VH. Определим булеву функцию fH, Положив fH (x)=0 для n-мерного (0, 1)-вектора х = хv Тогда и только тогда, когда U € ГH. Поскольку любое подмножество независимого множества также независимо, то функция fH монотонна и fn (0, 0, ..., 0) = 0.
Соответствие Н -> fH не является, вообще говоря, инъективным, поскольку ребра гиперграфа могут содержаться одно в другом. Поэтому определенный интерес представляют гиперграфы специального вида — антицепи. Гиперграф называется антицепью, если никакое из его ребер в является подмножеством другого ребра. Очевидно, что все k-однородные гиперграфы и, в частности, все простые графы — антицепи.
Пусть Н — произвольная антицепь с непустым множеством ребер, VH = {1, 2, ..., п). Очевидно, что характеристические векторы ребер гиперграфа Н попарно несравнимы относительно порядка ≤: x=( х1, х2, ..., хп)≤  y=( y1, y2, ..., yп) <=> (xi ≤ yi i = 1, п). Поэтому существует единственная монотонная булева функция п переменных, множество нижних единиц которой совпадает с множеством всех характеристических векторов ребер гиперграфа H. Очевидно, что fH и есть такая функция. Для антицепи, не имеющей ребер, fH = 0.
y=( y1, y2, ..., yп) <=> (xi ≤ yi i = 1, п). Поэтому существует единственная монотонная булева функция п переменных, множество нижних единиц которой совпадает с множеством всех характеристических векторов ребер гиперграфа H. Очевидно, что fH и есть такая функция. Для антицепи, не имеющей ребер, fH = 0.
С другой стороны, пусть f — монотонная булева функция п переменных, f ≠ 1. Определим гиперграф Hf, положив VHf = {1, 2, ..., п) и объявив ребрами все подмножества в VHf, характеристические векторы которых служат нижними единицами функции fH. Поскольку эта функция монотонна, то гиперграф Hf окажется антицепью. Очевидно, что fH f = f.
Итак, соответствие f -> Hf — биекция между множеством монотонных булевых функций, отличных от тождественно равной 1, и множеством антицепей.
 |
Пусть теперь А — произвольная m X n-матрица без нулевых столбцов, элементы которой — неотрицательные вещественные числа. Рассмотрим систему линейных неравенств
Здесь X — столбец неизвестных x1, x2 ,.. ,xn, В — столбец высоты m с неотрицательными элементами. Нас будут интересовать (0, 1)-решения этой системы. Определим булеву функцию f п переменных, положив f(x1, x2 ,.. ,xn) = 0 тогда и только тогда, когда (x1, x2 ,.. ,xn) — решение системы (1). Очевидно, что f — монотонная функция и f (0, 0, ..., 0) = 0. Скажем, что функция f задается системой неравенств (1).
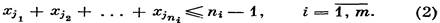 |
Легко понять, что любая монотонная булева функция, отличная от тождественно равной 1, задается некоторой системой линейных неравенств вида (1) с неотрицательными коэффициентами и правыми частями. В самом деле, пусть f — такая функция, Hf — соответствующая антицепь, VHf = (1, 2, ..., п), EHf = {e1 , е2, ...., еm },|ei| = ni (i = 1, m). Рассмотрим систему неравенств
Очевидно, что вектор х = xU = (x1, x2 ,.. ,xn) — решение этой системы тогда и только тогда, когда U € SH. Последнее означает, что fH f = 0. Но fHf = f , следовательно, функция f задается системой (2).
Если же антицепь Hi не имеет ребер, т. е. если f=0, то в качестве системы неравенств (2) можно взять систему xi ≤ 1 (i = 1, п).
Очевидно, что система неравенств, задающая монотонную булеву функцию, определяется неоднозначно.
Из всего сказанного выше очевидно вытекает следующее
Утверждение 69.1. Пусть f — монотонная булева функция, отличная от тождественно равной 1, (1)—задающая эту функцию система линейных неравенств, Hf — соответствующая антицепь, VHf = (1, 2, ...,п), U € VHf, xU — характеристический вектор подмножества U. Тогда следующие высказывания эквивалентны:
1) f (xU)=0;
2) вектор xU является решением системы (1);
3) U€ГHf.
Для того частного случая, когда все нижние единицы функции f имеют норму 2 (функция f графическая), указанная связь между функциями, системами неравенств и антицепями отмечалась ранее в § 28. В этой и только в этой ситуации антицепь Hf является простым графом.
В точности так же, как и для графов, определяется пороговое число th(Н) произвольной антицепи Н. Но в общем случае этот важный параметр изучался мало.
Раскраски
Так же, как для графов, вводится понятие вершинной раскраски гиперграфов. Раскраска вершин гиперграфа Н называется правильной, если любое ребро е = EH содержит две вершины, окрашенные в различные цвета. Ясно, что правильную раскраску могут допускать лишь гиперграфы, каждое ребро которых имеет степень не меньше чем 2. В этом параграфе рассматриваются только такие типерграфы. Кроме того, будем считать, что изолированных вершин гиперграф не содержит.
Гиперграф называется k-раскрашиваемым (k-цветным), если для него существует правильная раскраска в k цветов.
Хроматическое число χ(H) — это наименьшее число цветов, достаточное для правильной раскраски гиперграфа Н. Если χ(Н)=k, то гиперграф Н называется к-хроматическим.
Очевидно, что разбиению множества VH на независимые множества S1, S2, ..., Sk соответствует правильная раскраска вершин гиперграфа Н k цветами. Верно, конечно, и обратное утверждение.
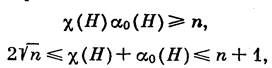 |
Теорема 70.1. Для любого гиперграфа Н порядка п справедливы неравенства
где αо(Н)— число независимости гиперграфа Н.
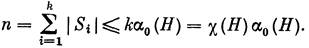 |
Рассмотрим разбиение множества VH на независимые множества S1, S2, ..., Sk где k = χ(Н). Тогда будем иметь
Отсюда сразу получаем χ(Н)+ αо(Н)> 2√п
Далее, пусть S — наибольшее независимое множество вершин гиперграфа Н. Окрасим все вершины из S в один цвет и используем п — |S| = п — αо(Н) других цветов для окрашивания всех вершин из V \ S в разные цвета» В результате получаем χ(Н) + ао(Н)≤ п+ 1.
Важное место в теории графов занимают верхние оценки хроматического числа в терминах степеней вершин. При естественном определении степени вершин сохраняет силу теорема Брукса. При другом определении, которое мы дадим ниже, получается более тонкая оценка хроматического числа, полученная И. Томеску.
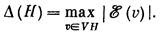 |
Так же, как и для графов, через Δ(Н) будем обозначать наибольшую из степеней вершин гиперграфа Н:
Абсолютным гиперграфом будем называть гиперграф для любых двух вершин и и v которого существует ребра е = uv. Оказывается, справедлива следующая теорема, являющаяся обобщением теоремы Брукса (§ 54).
Теорема 70.2 (Л. Ловас, 1968 г.). Если Н — связный гиперграф, отличный от абсолютного, и Δ(Н) ≥ 3, то χ(H)≤(Н).
Порядком dH (v) вершины v гиперграфа Н называется мощность наибольшего подмножества E' €EН, |E’| ≥ 2, для любых двух различных ребер е' в е" которого е' ∩ е" = {v}. Если такого подмножества не существует, то по определению dH(v)= 1.
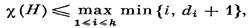 |
Теорема 70.3 (И. Томеску, 1968 г.). Пусть S1, S2, ..., Sk — разбиение множества VH на независимые множества. Тогда
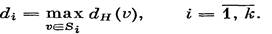 |
Где
Доказательства двух предыдущих теорем опускаем. Если |Si| = 1 ( i = 1, k), то учитывая очевидное неравенство Δ(Н)≥ d(H), где d(H)= max dH(v), получаем
Следствие 70.4. Для любого гиперграфа Н верно неравенство
χ(H) ≤ d(H)+1.
Отсюда сразу имеем (ср. со следствием 54.2) Следствие 70.5. Для любого гиперграфа Н верно неравенство
χ(H) ≤ Δ(H)+1
На первый взгляд кажется, что наличие ребер высокой степени должно способствовать снижению хроматического числа гиперграфа. Однако это не так, как показывает следующая
Теорема 70.6. Для любых целых чисел k ≥ 1 и h ≥ 2 существует такой гиперграф Н, что χ(Н)≥ k и |е| ≥ h для любого ребра е € EH.
В качестве такого гиперграфа можно взять h-однородный гиперграф Н, построенный по следующему правилу: VH = {v1, v2, ..., vn} где n ≥ k(h — 1), ЕH — семейство всевозможных подмножеств множества VH мощности h. Поскольку ао(Н) ≤ h— 1, то на основании теоремы 70.1 χ(H)≥n/(h-l), т. е. χ(H)≥ k.
Более сильный результат приведем без доказательства.
Теорема 70.7 (П. Эрдёш, А. Хайнал, 1966 г.). Для любых целых чисел h, k, l≥2 существует h-однородный k-хроматический гиперграф, который не содержит циклов длины меньше l.
Известно, какую роль в теории графов играют бихроматические графы, т. е. графы, хроматическое число которых не превосходит 2. Простой, но очень важный критерий бихроматичности графа дал Д. Кёниг: граф не должен содержать циклов нечетной длины.
Гиперграф Н тоже будем называть бихроматическим, если χ(H)≤2. Для гиперграфа пока не найдено критерия бихроматичности в терминах его структуры.
 |
Утверждение 70.8. Если гиперграф не содержит циклов нечетной длины, то он является бихроматическим.
Доказательство проводим по той же схеме, что и доказательство теоремы 9.1, предполагая, что гиперграф
связен. А именно, сначала окрасим произвольную вершину v гиперграфа Н в красный цвет, затем произвольную вершину и, отличную от v, окрасим в красный цвет, если расстояние d(u, v) — четное число, и в синий цвет, если это расстояние нечетно. Если Н — не бихроматический гиперграф, то найдутся две смежные вершины и и w, окрашенные в один цвет, а тогда легко обнаруживается цикл нечетной длины.
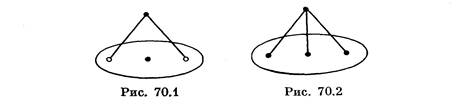
Как показывает пример гиперграфа, изображенного на рис. 70.1, условие утверждения 70.8 не являются необходимыми.
Более широкий класс бихроматических графов нашли Фурнье и Лас Верньяс. Этот результат приведем без доказательства.
Теорема 70.9 (Ж. Фурнье, М. Лас Верпьяс, 1972). Если в каждом цикле нечетной длины гиперграфа Н есть три ребра, имеющие общую инцидентную вершину, то гиперграф Н является бихроматическим.
Пример гиперграфа на рис. 70.1 показывает, что это достаточное условие также не является необходимым.
Непосредственно из теоремы Кёнига следует
Утверждение 70.10. Если гиперграф является бихроматическим, то он не содержит ни одного цикла нечетной длины, состоящего лишь из ребер степени 2.
Пример гиперграфа, изображенного на рис. 70.2, показывает, что обратное утверждение неверно.
Доказательства теорем, опущенные в этом параграфе, можно найти в [20].
Дата добавления: 2019-07-26; просмотров: 404;
